1.6 Exercises
The exercises in this book are based on code available from Packt Publishing on GitHub. See https://github.com/PacktPublishing/Functional-Python-Programming-3rd-Edition.
In some cases, the reader will notice that the code provided on GitHub includes partial solutions to some of the exercises. These serve as hints, allowing the reader to explore alternative solutions.
In many cases, exercises will need unit test cases to confirm they actually solve the problem. These are often identical to the unit test cases already provided in the GitHub repository. The reader will need to replace the book’s example function name with their own solution to confirm that it works.
1.6.1 Convert an imperative algorithm to functional code
The following algorithm is stated as imperative assignment statements and a while construct to indicate processing something iteratively.

What does this appear to compute? Given Python built-in functions like sum, can this be simplified?
It helps to write this in Python and refactor the code to be sure that correct answers are created.
A test case is the following:
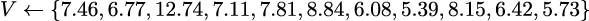
The computed value for m is approximately 7.5.
1.6.2 Convert step-wise computation to functional code
The following algorithm is stated as a long series of single assignment statements. The rad(x) function converts degrees to radians, rad(d) = π × . See the
. See the math module for an implementation.

Is this code easy to understand? Can you summarize this computation as a short mathematical-looking formula?
Breaking it down into sections, lines 1 to 8 seem to be focused on some conversions, differences, and mid-point computations. Lines 9 to 12 compute two values, x and y. Can these be summarized or simplified? The final four lines do a relatively direct computation of d. Can this be summarized or simplified? As a hint, look at math.hypot() for a function that might be applicable in this case.
It helps to write this in Python and refactor the code.
A test case is the following:
lon1 ←−79.93021
lat2 ← 32.74412
lon2 ←−79.85226
The computed value for d is approximately 6.4577.
Refactoring the code can help to confirm your understanding.
1.6.3 Revise the sqrt() function
The sqrt() function defined in the A classic example of functional programming section has only a single parameter value, n. Rewrite this to create a more advanced version using default parameter values to make changes possible. An expression such as sqrt(1.0, 0.000_01, 3) will start with an approximation of 1.0 and compute the value to a precision of 0.00001. The final parameter value, 3, is the value of n, the number we need to compute the square root of.
1.6.4 Data cleansing steps
A file of source data has US ZIP codes in a variety of formats. This problem often arises when spreadsheet software is used to collect or transform data.
Some ZIP codes were processed as numbers. This doesn’t work out well for places in New England, where ZIP codes have a leading zero. For example, one of Portsmouth, New Hampshire’s codes should be stated as
03801. In the source file, it is3801. For the most part, these numbers will have five or nine digits, but some codes in New England will be four or eight digits when a single leading zero was dropped. For Puerto Rico, there may be two leading zeroes.Some ZIP codes are stored as strings, 12345−0100, where a four-digit extension for a post-office box has been appended to the base five-digit code.
A CSV-format file has only text values. However, when data in the file has been processed by a spreadsheet, problems can arise. Because a ZIP code has only digits, it can be treated as numeric data. This means the original data values will have been converted to a number, and then back to a text representation. These conversions will drop the leading zeroes. There are a number of workarounds in various spreadsheet applications to prevent this problem. If they’re not used, the data can have anomalous values that can be cleansed to restore the original representation.
The objective of the exercise is to compute a histogram of the most popular ZIP codes in the source data file. The data must be cleansed to have the following two ZIP formats:
Five characters with no post-office box, for example
03801Ten characters with a hyphen, for example
03899-9876
The essential histogram can be done with a collections.Counter object as follows.
from collections import Counter
import csv
from pathlib import Path
DEFAULT_PATH = Path.cwd() / "address.csv"
def main(source_path: Path = DEFAULT_PATH) -> None:
frequency: Counter[str] = Counter()
with source_path.open() as source:
rdr = csv.DictReader(source)
for row in rdr:
if "-" in row[’ZIP’]:
text_zip = row[’ZIP’]
missing_zeroes = 10 - len(text_zip)
if missing_zeroes:
text_zip = missing_zeroes*’0’ + text_zip
else:
text_zip = row[’ZIP’]
if 5 < len(row[’ZIP’]) < 9:
missing_zeroes = 9 - len(text_zip)
else:
missing_zeroes = 5 - len(text_zip)
if missing_zeroes:
text_zip = missing_zeroes*’0’ + text_zip
frequency[text_zip] += 1
print(frequency)
if __name__ == "__main__":
main()This makes use of imperative processing features to read a file. The overall design, using a for statement to process rows of a file, is an essential Pythonic feature that we can preserve.
On the other hand, the processing of the text_zip and missing_zeroes variables through a number of state changes seems like it’s a potential source for confusion.
This can be refactored through several rewrites:
Decompose the
main()function into two parts. A newzip_histogram()function should be written to contain much of the processing detail. This function will process the opened file, and return aCounterobject. A suggested signature is the following:def zip_histogram( reader: csv.DictReader[str]) -> Counter[str]: passThe
main()function is left with the responsibility to open the file, create thecsv.DictReaderinstance, evaluatezip_histogram(), and print the histogram.Once the
zip_histogram()function has been defined, the cleansing of theZIPattribute can be refactored into a separate function, with a name likezip_cleanse(). Rather than setting the value of thetext_zipvariable, this function can return the cleansed result. This can be tested separately to be sure the various cases are handled gracefully.The distinction between long ZIP codes with a hyphen and without a hyphen is something that should be fixed. Once the
zip_cleanse()works in general, add a new function to inject hyphens into ZIP codes with only digits. This should transform38011234to03801-1234. Note that short, five-digit ZIP codes do not need to have a hyphen added; this additional transformation only applies to nine-digit codes to make them into ten-position strings.
The final zip_histogram() function should look something like the following:
def zip_histogram(
reader: csv.DictReader[str]) -> Counter[str]:
return Counter(
zip_cleanse(
row[’ZIP’]
) for row in reader
)This provides a framework for performing a focused data cleanup in the given column. It allows us to distinguish between CSV and file processing features, and the details of how to clean up a specific column of data.
1.6.5 (Advanced) Optimize this functional code
The following algorithm is stated as a single ”step” that has been decomposed into three separate formulae. The decomposition is more a concession to the need to fit the expression into the limits of a printed page than a useful optimization. The rad(x) function converts degrees to radians, rad(d) = π × .
.

There are a number of redundant expressions, like rad(lat1) and rad(lat2). If these are assigned to local variables, can the expression be simplified?
The final computation of d does not match the conventional understanding of computing a hypotenuse,  . Should the code be refactored to match the definition in
. Should the code be refactored to match the definition in math.hypot?
It helps to start by writing this in Python and then refactoring the code.
A test case is the following:
lon1 ←−79.93021
lat2 ← 32.74412
lon2 ←−79.85226
The computed value for d is approximately 6.4577.
Refactoring the code can help to confirm your understanding of what this code really does.

























































