5.7 Bayes factors and inference
So far, we have used Bayes factors to judge which model seems to be better at explaining the data, and we found that one of the models is ≈ 5 times better than the other.
But what about the posterior we get from these models? How different are they? Table 5.2 summarizes these two posteriors:
| mean | sd | hdi_3% | hdi_97% | |
| uniform | 0.5 | 0.05 | 0.4 | 0.59 |
| peaked | 0.5 | 0.04 | 0.42 | 0.57 |
Table 5.2: Statistics for the models with uniform and peaked priors computed using the ArviZ summary function
We can argue that the results are quite similar; we have the same mean value for θ and a slightly wider posterior for model_0, as expected since this model has a wider prior. We can also check the posterior predictive distribution to see how similar they are (see Figure 5.13).
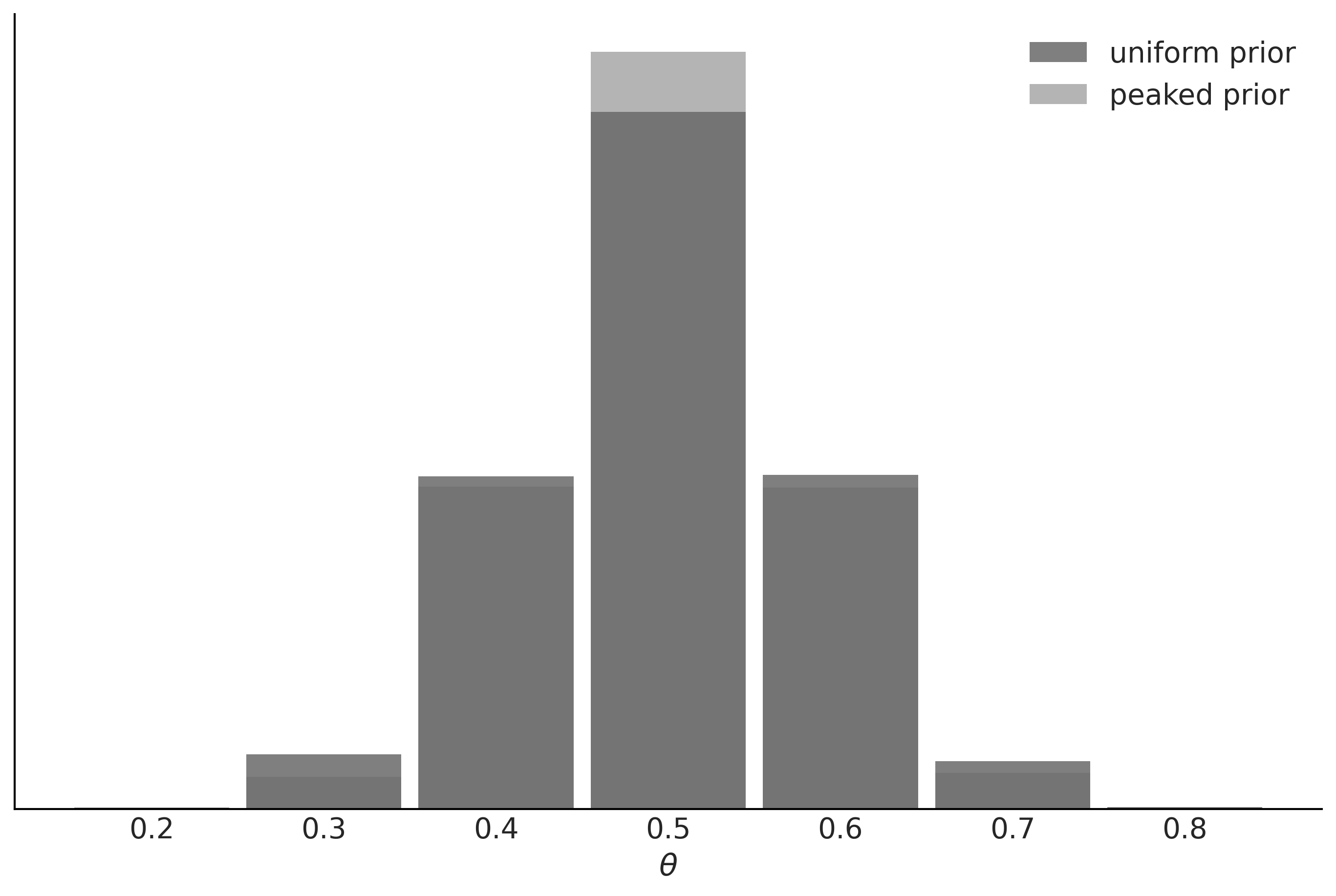
Figure 5.13: Posterior predictive distributions for models with uniform and peaked priors
In this example, the observed data is more consistent with model_1, because the prior...























































