Relational algebra
Relational algebra is the formal language of the relational model. It defines a set of closed operations over relations, that is, the result of each operation is a new relation. Relational algebra inherits many operators from set algebra. Relational algebra operations could be categorized into two groups:
- The first one is a group of operations which are inherited from set theory such as
UNION,INTERSECTION,SET DIFFERENCE, andCARTESIAN PRODUCT, also known asCROSS PRODUCT. - The second is a group of operations which are specific to the relational model such as
SELECTandPROJECT.
Relational algebra operations could also be classified as binary and unary operations. Primitive relational algebra operators have ultimate power of reconstructing complex queries. The primitive operators are:
SELECT(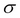 ): A unary operation written as
): A unary operation written as 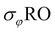 where
where 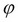 is a predicate. The selection retrieves the tuples in R, where
is a predicate. The selection retrieves the tuples in R, where 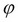 holds.
holds.
PROJECT(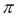 ): A unary operation used to slice the relation in a vertical dimension, that is, attributes. This operation is written as
): A unary operation used to slice the relation in a vertical dimension, that is, attributes. This operation is written as  , where
, where  are a set of attribute names.
are a set of attribute names.
CARTESIAN PRODUCT(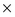 ): A binary operation used to generate a more complex relation by joining each tuple of its operands together. Let us assume that R and S are two relations, then
): A binary operation used to generate a more complex relation by joining each tuple of its operands together. Let us assume that R and S are two relations, then 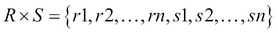 , where
, where 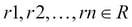 and
and 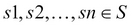 .
.
UNION( ): Appends two relations together; note that the relations should be union compatible, that is, they should have the same set of ordered attributes. Formally,
): Appends two relations together; note that the relations should be union compatible, that is, they should have the same set of ordered attributes. Formally,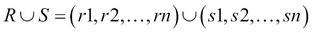 , where
, where  and
and 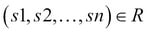 .
.
DIFFERENCE( or
or -): A binary operation in which the operands should be union compatible. Difference creates a new relation from the tuples, which exist in one relation but not in the other. The set difference for the relation R and S can be given as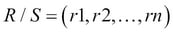 , where
, where  and
and 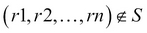 .
.
RENAME(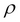 ): A unary operation that works on attributes. It simply renames an attribute. This operator is mainly used in JOIN operations to distinguish the attributes with the same names but in different relation tuples. Rename is expressed as
): A unary operation that works on attributes. It simply renames an attribute. This operator is mainly used in JOIN operations to distinguish the attributes with the same names but in different relation tuples. Rename is expressed as 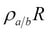 .
.
In addition to the primitive operators, there are aggregation functions such as sum, count, min, max, and average aggregates. Primitive operators can be used to define other relation operators such as left-join, right-join, equi-join, and intersection. Relational algebra is very important due to its expressive power in optimizing and rewriting queries. For example, the selection is commutative, so 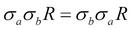 . A cascaded selection may also be replaced by a single selection with a conjunction of all the predicates, that is,
. A cascaded selection may also be replaced by a single selection with a conjunction of all the predicates, that is,  .
.
The SELECT and PROJECT operations
SELECT is used to restrict tuples from the relation. If no predicate is given then the whole set of tuples is returned. For example, the query "give me the customer information where the customer_id equals to 2" is written as:

The selection is commutative; the query "give me all customers where the customer mail is known, and the customer first name is kim" is written in three different ways, as follows:



The selection predicates are certainly determined by the data types. For numeric data types, the comparison operator might be (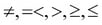 ). The predicate expression can contain complex expressions and functions.
). The predicate expression can contain complex expressions and functions.
The equivalent SQL statement for the SELECT operator is the SELECT * statement, and the predicate is defined in the WHERE clause. Finally, the * means all the relation attributes; note that in the production environment, it is not recommended to use *. Instead, one should list all the relation attributes explicitly.
SELECT * FROM customer WHERE customer_id=2
The project operation could be visualized as vertical slicing of the table. The query: "give me the customer names" is written in relational algebra as follows:

|
first_name |
last_name |
|---|---|
|
Thomas |
Baumann |
|
Wang |
Kim |
|
Christian |
Bayer |
|
Ali |
Ahmad |
The result of project operation
Duplicate tuples are not allowed in the formal relational model; the number of returned tuples from the project operator is always equal to or less than the number of total tuples in the relation. If a project operator's attribute list contains a primary key, then the resulting relation has the same number of tuples as the projected relation.
Cascading projections could be optimized as the following expression:

The SQL equivalent for the PROJECT operator in SQL is SELECT DISTINCT. The DISTINCT keyword is used to eliminate duplicates. To get the result shown in the preceding expression, one could execute the following SQL statement:
SELECT DISTINCT first_name, last_name FROM customers;
The sequence of the execution of the PROJECT and SELECT operations can be interchangeable in some cases.
The query "give me the name of the customer with customer_id equal to 2" could be written as:


In other cases, the PROJECT and SELECT operators must have an explicit order as shown in the following example; otherwise, it will lead to an incorrect expression. The query "give me the last name of the customers where the first name is kim" could be written as the following expression:

The RENAME operation
The Rename operation is used to alter the attribute name of the resultant relation, or to give a specific name to the resultant relation. The Rename operation is used to:
- Remove confusion if two or more relations have attributes with the same name
- Provide user-friendly names for attributes, especially when interfacing with reporting engines
- Provide a convenient way to change the relation definition, and still be backward compatible
The AS keyword in SQL is the equivalent of the RENAME operator in relational algebra. the following SQL example creates a relation with one tuple and one attribute, which is renamed PI.
SELECT 3.14::real AS PI;
The Set theory operations
The set theory operations are union, intersection, and minus (difference). Intersection is not a primitive relational algebra operator, because it is can be written using the union and difference operators:

The intersection and union are commutative:


For example, the query "give me all the customer IDs where the customer does not have a service assigned to him" could be written as:

The CROSS JOIN (Cartesian product) operation
The CROSS JOIN operation is used to combine tuples from two relations into a single relation. The number of attributes in a single relation equals the sum of the number of attributes of the two relations. The number of tuples in the single relation equals the product of the number of tuples in the two relations. Let us assume A and B are two relations, and 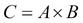 . Then:
. Then:


The following image shows the cross join of customer and customer service, that is,  :
:
|
customer.customer_id |
first_name |
last_name |
|
phone |
customer_service.customer_id |
service_id |
start_date |
end_date |
|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
CROSS JOIN of customer and customer_service relations
For example, the query "for the customer with customer_id equal to 3, retrieve the customer name and the customer service IDs" could be written in SQL as follows:
SELECT first_name, last_name, service_id FROM customer AS c CROSS JOIN customer_service AS cs WHERE c.customer_id=cs.customer_id AND c.customer_id = 3;
In the preceding example, one can see the relationship between relational algebra and the SQL language. It shows how relational algebra could be used to optimize query execution. This example could be executed in several ways, such as:
Execution plan 1:
- Select the customer where
customer_id = 3. - Select the customer service where
customer_id = 3. - Cross JOIN the relations resulting from steps 1 and 2.
- Project
first_name,last_name, andservice_idfrom the relation resulting from step 3
Execution plan 2:
- Cross JOIN
customerandcustomer_service - Select all the tuples where
Customer_service.customer_id=customer.customer_idandcustomer.customer_id = 3 - Project
first_name,last_name, andservice_idfrom the relation resulting from step 2.
Each execution plan has a cost in terms of CPU and hard disk operations. The RDBMS picks the one with the lowest cost. In the preceding execution plans, the RENAME operator was ignored for simplicity.
























































