2.1 Probabilistic programming

Bayesian statistics is conceptually very simple. We have the knowns and the unknowns, and we use Bayes’ theorem to condition the latter on the former. If we are lucky, this process will reduce the uncertainty about the unknowns. Generally, we refer to the knowns as data and treat it like constants, and the unknowns as parameters and treat them as random variables.

Although conceptually simple, fully probabilistic models often lead to analytically intractable expressions. For many years, this was a real problem and one of the main issues that hindered the adoption of Bayesian methods beyond some niche applications. The arrival of the computational era and the development of numerical methods that, at least in principle, can be used to solve any inference problem, have dramatically transformed the Bayesian data analysis practice. We can think of these numerical methods as universal inference engines. The possibility of automating the inference process has led to the development of probabilistic programming languages (PPLs), which allows a clear separation between model creation and inference. In the PPL framework, users specify a full probabilistic model by writing a few lines of code, and then inference follows automatically.

It is expected that probabilistic programming will have a major impact on data science and other disciplines by enabling practitioners to build complex probabilistic models in a less time-consuming and less error-prone way. I think one good analogy for the impact that programming languages can have on scientific computing is the introduction of the Fortran programming language more than six decades ago. While nowadays Fortran has lost its shine, at one time, it was considered revolutionary. For the first time, scientists moved away from computational details and began focusing on building numerical methods, models, and simulations more naturally. It is interesting to see that some folks are working on making Fortran cool again, if you are interested you can check their work at https://fortran-lang.org/en.

2.1.1 Flipping coins the PyMC way

Let’s revisit the coin-flipping problem from Chapter 1, but this time using PyMC. We will use the same synthetic data we used in that chapter. Since we are generating the data, we know the true value of θ, called theta_real, in the following block of code. Of course, for a real dataset, we will not have this knowledge:

Code 2.1

np.random.seed(123) 
 
trials = 4 
theta_real = 0.35 # unknown value in a real experiment 
data = pz.Binomial(n=1, p=theta_real).rvs(trials)

Now that we have the data, we need to specify the model. Remember that this is done by specifying the likelihood and the prior. For the likelihood, we will use the Binomial distribution with parameters n = 1, p = θ, and for the prior, a Beta distribution with the parameters α = β = 1. A Beta distribution with such parameters is equivalent to a Uniform distribution on the interval [0, 1]. Using mathematical notation we can write the model as:

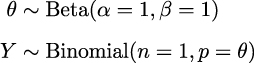
This statistical model has an almost one-to-one translation to PyMC:

Code 2.2

with pm.Model() as our_first_model: 
    θ = pm.Beta('θ', alpha=1., beta=1.) 
    y = pm.Bernoulli('y', p=θ, observed=data) 
    idata = pm.sample(1000)

The first line of the code creates a container for our model. Everything inside the with block will be automatically added to our_first_model. You can think of this as syntactic sugar to ease model specification as we do not need to manually assign variables to the model. The second line specifies the prior. As you can see, the syntax follows the mathematical notation closely. The third line specifies the likelihood; the syntax is almost the same as for the prior, except that we pass the data using the observed argument. The observed values can be passed as a Python list, a tuple, a NumPy array, or a pandas DataFrame. With that, we are finished with the model specification! Pretty neat, right?

We still have one more line of code to explain. The last line is where the magic happens. Behind this innocent line, PyMC has hundreds of oompa loompas singing and baking a delicious Bayesian inference just for you! Well, not exactly, but PyMC is automating a lot of tasks. For the time being, we are going to treat that line as a black box that will give us the correct result. What is important to understand is that under the hood we will be using numerical methods to compute the posterior distribution. In principle, these numerical methods are capable of solving any model we can write. The cost we pay for this generality is that the solution is going to take the form of samples from the posterior. Later, we will be able to corroborate that these samples come from a Beta distribution, as we learned from the previous chapter. Because the numerical methods are stochastic, the samples will vary every time we run them. However, if the inference process works as expected, the samples will be representative of the posterior distribution and thus we will obtain the same conclusion from any of those samples. The details of what happens under the hood and how to check if the samples are indeed trustworthy will be explained in Chapter 10.

One more thing: the idata variable is an InferenceData object, which is a container for all the data generated by PyMC. We will learn more about this later in this chapter.

OK, so on the last line, we are asking for 1,000 samples from the posterior. If you run the code, you will get a message like this:

Auto-assigning NUTS sampler... Initializing NUTS using jitter+adapt_diag... Multiprocess sampling (4 chains in 4 jobs)
NUTS: [θ]
Sampling 4 chains for 1_000 tune and 1_000 draw iterations (4_000 + 4_000 draws total) took 1 second.

The first and second lines tell us that PyMC has automatically assigned the NUTS sampler (one inference engine that works very well for continuous variables), and has used a method to initialize that sampler (these methods need some initial guess of where to start sampling). The third line says that PyMC will run four chains in parallel, thus we will get four independent samples from the posterior. As PyMC attempts to parallelize these chains across the available processors in your machine, we will get the four for the price of one. The exact number of chains is computed taking into account the number of processors in your machine; you can change it using the chains argument for the sample function. The next line tells us which variables are being sampled by which sampler. For this particular case, this line is not adding new information because NUTS is used to sample the only variable we have, θ. However, this is not always the case because PyMC can assign different samplers to different variables. PyMC has rules to ensure that each variable is associated with the best possible sampler. Users can manually assign samplers using the step argument of the sample function, but you will hardly need to do that.

Finally, the last line is a progress bar, with several related metrics indicating how fast the sampler is working, including the number of iterations per second. If you run the code, you will see the progress bar get updated really fast. Here, we are seeing the last stage when the sampler has finished its work. You will notice that we have asked for 1,000 samples, but PyMC is computing 8,000 samples. We have 1,000 draws per chain to tune the sampling algorithm (NUTS, in this example). These draws will be discarded by default; PyMC uses them to increase the efficiency and reliability of the sampling method, which are both important to obtain a useful approximation to the posterior. We also have 1,000 productive draws per chain for a total of 4,000. These are the ones we are going to use as our posterior. We can change the number of tuning steps with the tune argument of the sample function and the number of draws with the draw argument.

Faster Sampling

Under the hood, PyMC uses PyTensor, a library that allows one to define, optimize, and efficiently evaluate mathematical expressions involving multi-dimensional arrays. PyTensor significantly enhances the speed and performance of PyMC. Despite the advantages, it’s worth noting that the samplers in PyMC are implemented in Python, which may result in slower execution at times. To address this limitation, PyMC allows external samplers. I recommend using nutpie, a sampler written in Rust. For more information on how to install and call nutpie from PyMC, please check Chapter 10.