Classifying simulation models
Simulation models can be classified according to different criteria. The first distinction is between static and dynamic systems. So, let’s see what differentiates them.
Comparing static and dynamic models
A system is an object with a finite number of degrees of freedom that evolves over time according to a deterministic law. A system can be represented as a black box that can be stimulated by a stress (input) x (t) and that produces an effect (output) y (t). The behavior of the system is fully described by the following equation:

Static models are the representation of a system in an instant of time or representative models of a system in which the time variable plays no role. An example of a static simulation is a Monte Carlo model.
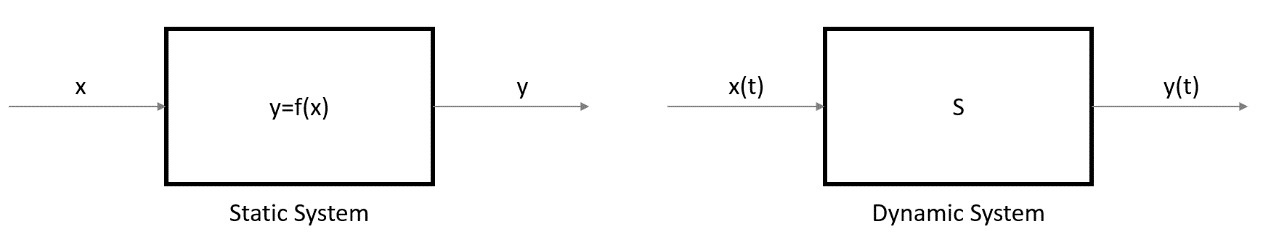
Figure 1.2: Static versus dynamic system representation
Dynamic models, on the other hand, describe the evolution of the system over time. In the simplest case, the state of the system at time t is described by a function x (t). For example, in population dynamics, x (t) represents the population present at time t. The equation that regulates the system is dynamic: it describes the instantaneous variation of the population or the variation in fixed time intervals.
Comparing deterministic and stochastic models
A model is deterministic when its evolution, over time, is uniquely determined by its initial conditions and characteristics. These models do not consider random elements and lend themselves to be solved with exact methods that are derived from mathematical analysis. In deterministic models, the output is well determined once the input data and the relationships that make up the model have been specified, despite the time required for data processing being particularly long. For these systems, the transformation rules univocally determine the change of state of the system. Examples of deterministic systems can be observed in some production and automation systems.
Stochastic models, on the other hand, can be evolved by inserting random elements into the evolution. These are obtained by extracting them from statistical distributions. Among the operational characteristics of these models, there is not just one relationship that fits all. There are also probability density functions, which means there is no one-to-one correspondence between the data and system history.
A final distinction is based on how the system evolves over time: therefore, we distinguish between continuous and discrete simulation models.
Comparing continuous and discrete models
Continuous models represent systems in which the state of the variables changes continuously as a function of time. For example, a car moving on a road represents a continuous system since the variables that identify it, such as position and speed, can change continuously with respect to time.
In discrete models, the system is described by an overlapping sequence of physical operations interspersed with inactivity pauses. These operations begin and end in well-defined instances (events). The system undergoes a change of state when each event occurs, remaining in the same state throughout the interval between the two subsequent events. This type of operation is easy to treat with the simulation approach.
Important note
The stochastic, deterministic, continuous, or discrete nature of a model is not its absolute property and depends on the observer’s vision of the system itself. This is determined by the objectives and the method of study, as well as by the experience of the observer.
Now that we’ve analyzed the different types of models in detail, we will learn how to develop a numerical simulation model.
























































