Basic plotting with Matplotlib
Plotting is an important part of understanding behavior. So much can be learned by simply plotting a function or data that would otherwise be hidden. In this recipe, we will walk through how to plot simple functions or data using Matplotlib, set the plotting style, and add labels to a plot.
Matplotlib is a very powerful plotting library, which means it can be rather intimidating to perform simple tasks with it. For users who are used to working with MATLAB and other mathematical software packages, there is a state-based interface called pyplot. There is also an object-oriented interface (OOI), which might be more appropriate for more complex plots. In either case, the pyplot interface is a convenient way to create basic objects.
Getting ready
Most commonly, the data that you wish to plot will be stored in two separate NumPy arrays, which we will label x and y for clarity (although this naming does not matter in practice). We will demonstrate plotting the graph of a function, so we will generate an array of x values and use the function to generate the corresponding y values. We’re going to plot three different functions over the range  on the same axes:
on the same axes:
def f(x): return x*(x - 2)*np.exp(3 – x) def g(x): return x**2 def h(x): return 1 - x
Let’s plot these three functions in Python using Matplotlib.
How to do it...
Before we can plot the function, we must generate x and y data to be plotted. If you are plotting existing data, you can skip these commands. We need to create a set of x values that cover the desired range, and then use the function to create y values:
- The
linspaceroutine from NumPy is ideal for creating arrays of numbers for plotting. By default, it will create 50 equally spaced points between the specified arguments. The number of points can be customized by providing an additional argument, but 50 is sufficient for most cases:x = np.linspace(-0.5, 3.0) # 50 values between -0.5 and 3.0
- Once we have created
xvalues, we can generateyvalues:y1 = f(x) # evaluate f on the x points
y2 = g(x) # evaluate g on the x points
y3 = h(x) # evaluate h on the x points
- To plot the data, we first need to create a new figure and attach axes objects, which can be achieved by calling the
plt.subplotsroutine without any arguments:fig, ax = plt.subplots()
Now, we use the plot method on the ax object to plot the first function. The first two arguments are  and
and  coordinates to be plotted, and the third (optional) argument specifies that the line color should be black:
coordinates to be plotted, and the third (optional) argument specifies that the line color should be black:
ax.plot(x, y1, "k") # black solid line style
To help distinguish the plots for the other functions, we plot those with a dashed line and a dot-dash line:
ax.plot(x, y2, "k--") # black dashed line style ax.plot(x, y3, "k.-") # black dot-dashed line style
Every plot should have a title and axis labels. In this case, there isn’t anything interesting to label the axes with, so we just label them "x" and "y":
ax.set_title("Plot of the functions f, g, and h")
ax.set_xlabel("x")
ax.set_ylabel("y")
Let’s also add a legend to help you distinguish between the different function plots without having to look elsewhere to see which line is which:
ax.legend(["f", "g", "h"])
Finally, let’s annotate the plot to mark the intersection between the functions  and
and  with text:
with text:
ax.text(0.4, 2.0, "Intersection")
This will plot the y values against the x values on a new figure. If you are working within IPython or with a Jupyter notebook, then the plot should automatically appear at this point; otherwise, you might need to call the plt.show function to make the plot appear:
plt.show()
If you use plt.show, the figure should appear in a new window. We won’t add this command to any further recipes in this chapter, but you should be aware that you will need to use it if you are not working in an environment where plots will be rendered automatically, such as an IPython console or a Jupyter Notebook. The resulting plot should look something like the plot in Figure 2.1:
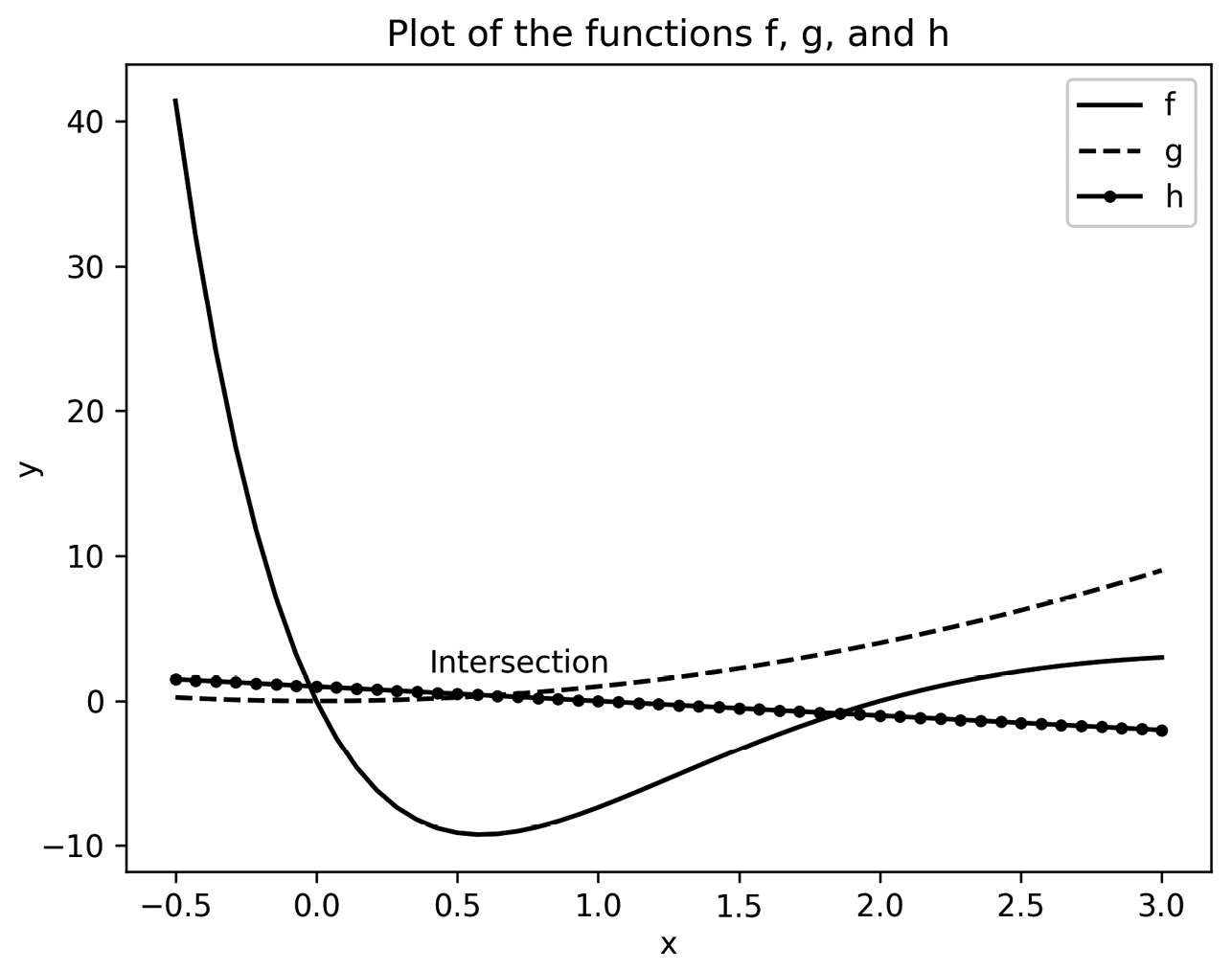
Figure 2.1 – Three functions on a single set of axes, each with a different style, with labels, legend, and an annotation
Note
If you are using a Jupyter notebook and the subplots command, you must include the call to subplots within the same cell as the plotting commands or the figure will not be produced.
How it works…
Here, we’re using the OOI because it allows us to keep track of exactly which figure and axes object we’re plotting on. This isn’t so important here where we have only a single figure and axes, but one can easily envisage situations where you might have two or more figures and axes concurrently. Another reason to follow this pattern is to be consistent when you add multiple subplots—see the Adding subplots recipe.
You can produce the same plot as in the recipe via the state-based interface by using the following sequence of commands:
plt.plot(x, y1, "k", x, y2, "k--", x, y3, "k.-")
plt.title("Plot of the functions f, g, and h")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(["f", "g", "h"])
plt.text(0.4, 2.0, "Intersection")
If there are currently no Figure or Axes objects, the plt.plot routine creates a new Figure object, adds a new Axes object to the figure, and populates this Axes object with the plotted data. A list of handles to the plotted lines is returned. Each of these handles is a Lines2D object. In this case, this list will contain a single Lines2D object. We could use this Lines2D object to further customize the appearance of the line later.
Notice that in the preceding code, we combined all the calls to the plot routine together. This is also possible if you use the OOI; the state-based interface is passing the arguments to the axes method on the set of axes that it either retrieves or creates.
The object layer of Matplotlib interacts with a lower-level backend, which does the heavy lifting of producing the graphical plot. The plt.show function issues an instruction to the backend to render the current figure. There are a number of backends that can be used with Matplotlib, which can be customized by setting the MPLBACKEND environment variable, modifying the matplotlibrc file, or by calling matplotlib.use from within Python with the name of an alternative backend. By default, Matplotlib picks a backend that is appropriate for the platform (Windows, macOS, Linux) and purpose (interactive or non-interactive), based on which backends are available. For example, on the author’s system, the QtAgg backend is the default. This is an interactive backend based on the Anti-Grain Geometry (AGG) library. Alternatively, one might want to use the QtCairo backend, which uses the Cairo library for rendering.
Note
The plt.show function does more than simply call the show method on a figure. It also hooks into an event loop to correctly display the figure. The plt.show routine should be used to display a figure, rather than the show method on a Figure object.
The format string used to quickly specify the line style has three optional parts, each consisting of one or more characters. The first part controls the marker style, which is the symbol that is printed at each data point; the second controls the style of the line that connects the data points; the third controls the color of the plot. In this recipe, we only specified the line style. However, one could specify both line style and marker style or just marker style. If you only provide the marker style, no connecting lines are drawn between the points. This is useful for plotting discrete data where no interpolation between points is necessary.
Four line-style parameters are available: a solid line (-), a dashed line (--), a dash-dot line (-.), or a dotted line (:). Only a limited number of colors can be specified in the format string; they are red, green, blue, cyan, yellow, magenta, black, and white. The character used in the format string is the first letter of each color (with the exception of black), so the corresponding characters are r, g, b, c, y, m, k, and w, respectively.
In the recipe, we saw three examples of these format strings: the single k format string only changed the color of the line and kept the other settings at default (small point markers and unbroken blue line); the k-- and k.- format strings both changed the color and the line style. For an example of changing the point style, see the There’s more... section and Figure 2.2:
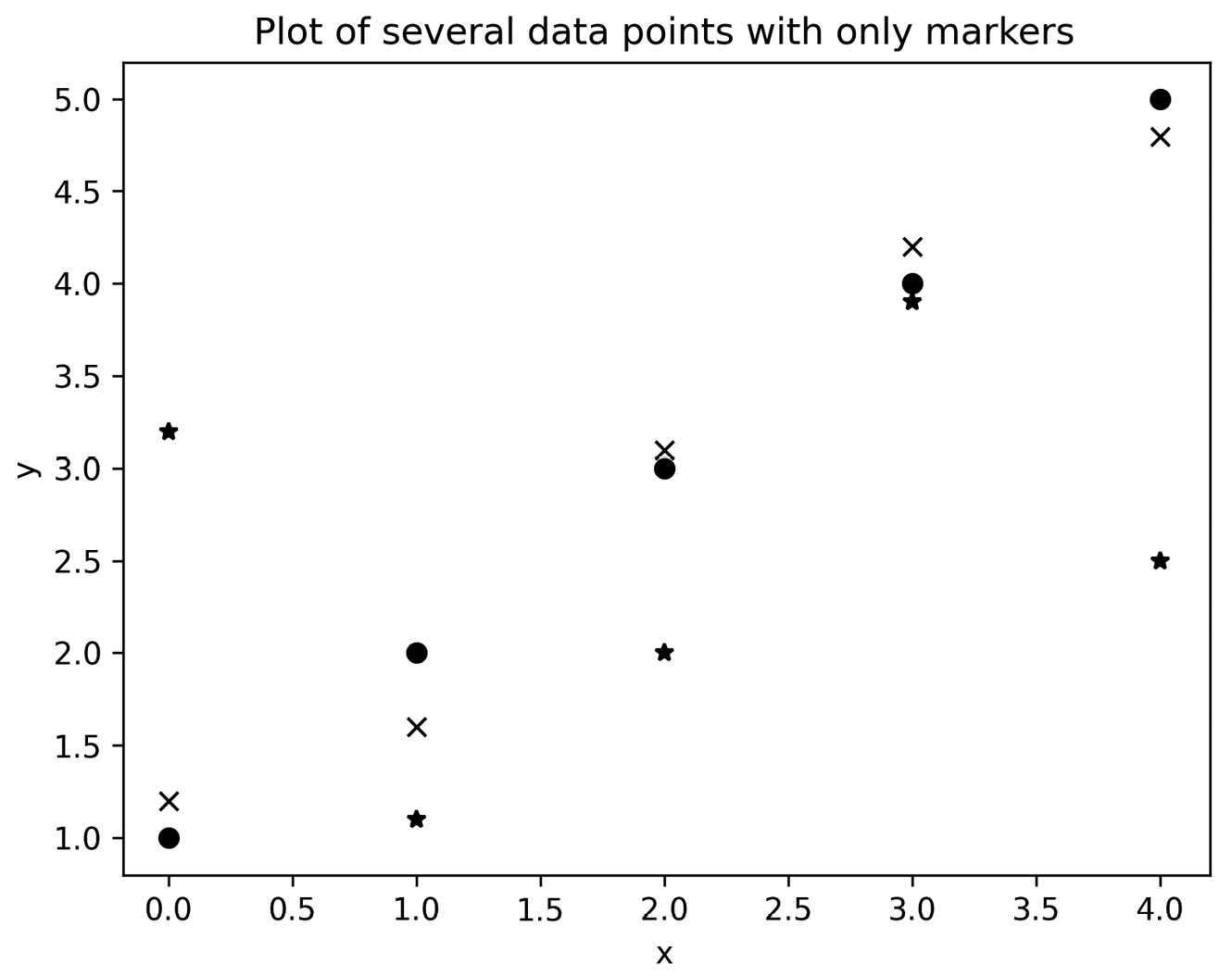
Figure 2.2 - Plot of three sets of data, each plotted using a different marker style
The set_title, set_xlabel, and set_ylabel methods simply add the text argument to the corresponding position of the Axes object. The legend method, as called in the preceding code, adds the labels to the datasets in the order that they were added to the plot—in this case, y1, y2, and then y3.
There are a number of keyword arguments that can be supplied to the set_title, set_xlabel, and set_ylabel routines to control the style of the text. For example, the fontsize keyword can be used to specify the size of the label font in the usual pt point measure.
The annotate method on the Axes object adds arbitrary text to a specific position on the plot. This routine takes two arguments—the text to display as a string and the coordinates of the point at which the annotation should be placed. This routine also accepts keyword arguments that can be used to customize the style of the annotation.
There’s more…
The plt.plot routine accepts a variable number of positional inputs. In the preceding code, we supplied two positional arguments that were interpreted as x values and y values (in that order). If we had instead provided only a single array, the plot routine would have plotted the values against their position in the array; that is, the x values are taken to be 0, 1, 2, and so on.
The plot method also accepts a number of keyword arguments that can also be used to control the style of a plot. Keyword arguments take precedence over format string parameters if both are present, and they apply to all sets of data plotted by the call. The keyword to control the marker style is marker, the keyword for the line style is linestyle, and the keyword for color is color. The color keyword argument accepts a number of different formats to specify a color, which includes RGB values as a (r, g, b) tuple, where each character is a float between 0 and 1 or is a hex string. The width of the line plotted can be controlled using the linewidth keyword, which should be provided with a float value. Many other keyword arguments can be passed to plot; a list is given in the Matplotlib documentation. Many of these keyword arguments have a shorter version, such as c for color and lw for linewidth.
In the this recipe, we plotted a large number of coordinates generated by evaluating functions on a selection of  values. In other applications, one might have data sampled from the real world (as opposed to generated). In these situations, it might be better to leave out the connecting lines and simply plot the markers at the points. Here is an example of how this might be done:
values. In other applications, one might have data sampled from the real world (as opposed to generated). In these situations, it might be better to leave out the connecting lines and simply plot the markers at the points. Here is an example of how this might be done:
y1 = np.array([1.0, 2.0, 3.0, 4.0, 5.0]) y2 = np.array([1.2, 1.6, 3.1, 4.2, 4.8]) y3 = np.array([3.2, 1.1, 2.0, 4.9, 2.5]) fig, ax = plt.subplots() ax.plot(y1, 'o', y2, 'x', y3, '*', color="k")
The result of these commands is shown in Figure 2.2. Matplotlib has a specialized method for producing scatter plots such as this, called scatter.
Other aspects of the plot can be customized by using methods on the Axes object. The axes ticks can be modified using the set_xticks and set_yticks methods on the Axes object, and the grid appearance can be configured using the grid method. There are also convenient methods in the pyplot interface that apply these modifications to the current axes (if they exist).
For example, we modify the axis limits, set the ticks at every multiple of 0.5 in both the  and
and  direction, and add a grid to the plot by using the following commands:
direction, and add a grid to the plot by using the following commands:
ax.axis([-0.5, 5.5, 0, 5.5]) # set axes ax.set_xticks([0.5*i for i in range(9)]) # set xticks ax.set_yticks([0.5*i for i in range(11)]) # set yticks ax.grid() # add a grid
Notice how we set the limits slightly larger than the extent of the plot. This is to avoid markers being placed on the boundary of the plot window.
Matplotlib has many other plotting routines besides the plot routine described here. For example, there are plotting methods that use a different scale for the axes, including the logarithmic  or
or  axes separately (
axes separately (semilogx or semilogy, respectively) or together (loglog). These are explained in the Matplotlib documentation. The scatter plotting routine may be useful if you wish to plot discrete data on axes without connecting the points with a line. This allows more control over the style of the marker. For example, you can scale the marker according to some additional information.
We can use a different font by using the fontfamily keyword, the value of which can be the name of a font or serif, sans-serif, or monospace, which will choose the appropriate built-in font. A complete list of modifiers can be found in the Matplotlib documentation for the matplotlib.text.Text class.
Text arguments can also be rendered using TeX for additional formatting by supplying usetex=True to the routine. We’ll demonstrate the use of TeX formatting of labels in Figure 2.3 in the following recipe. This is especially useful if the title or axis label contains a mathematical formula. Unfortunately, the usetex keyword argument cannot be used if TeX is not installed on the system—it will cause an error in this case. However, it is still possible to use the TeX syntax for formatting mathematical text within labels, but this will be typeset by Matplotlib, rather than by TeX.
























































