Graphs and distributions and how to map between them
In this section, we will focus on the mappings between the statistical and graphical properties of a system.
To be more precise, we’ll be interested in understanding how to translate between graphical and statistical independencies. In a perfect world, we’d like to be able to do it in both directions: from graph independence to statistical independence and the other way around.
It turns out that this is possible under certain assumptions.
The key concept in this chapter is one of independence. Let’s start by reviewing what it means.
How to talk about independence
Generally speaking, we say that two variables,  and
and  , are independent when our knowledge about
, are independent when our knowledge about  does not change our knowledge about
does not change our knowledge about  (and vice versa). In terms of probability distributions, we can express it in the following way:
(and vice versa). In terms of probability distributions, we can express it in the following way:

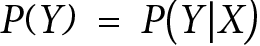
In other words: the marginal probability of  is the same as the conditional probability of
is the same as the conditional probability of  given...
given...























































