Medical tests – basic application of Bayes' theorem
A patient takes a special cancer test that has an accuracy of test_accuracy=99.9%—if the result is positive, then 99.9% of the patients tested will suffer from that particular type of cancer. Conversely, 99.9% of the patients with a negative result will not suffer from that particular cancer.
Suppose that a patient is tested and the result is positive. What is the probability of that patient suffering from that particular type of cancer?
Analysis
We will use Bayes' theorem to ascertain the probability of the patient having cancer:

To ascertain the prior probability that a patient has cancer, we have to find out how frequently cancer occurs among people. Say that we find out that 1 person in 100,000 suffers from this kind of cancer. Therefore, P(cancer)=1/100,000. So, P(test_positive|cancer) = test_accuracy=99.9%=0.999 given by the accuracy of the test.
P(test_positive) has to be computed as follows:


Therefore, we can calculate the following:


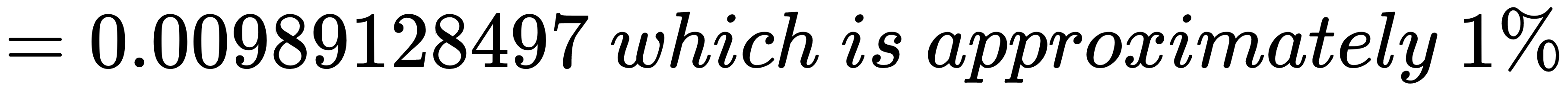
So...



























































