Appendix B. Probability
Essential concepts in probability are presented here in brief.
Axioms of probability
Kolmogorov's axioms of probability can be stated in terms of the sample space S of possible events, E1, E2, E3, …En and the real-valued probability P(E) of an event E. The axioms are:
- P(E) ≥ 0 for all E ϵ S
- P(S) = 1
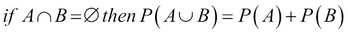
Together, these axioms say that probabilities cannot be negative numbers—impossible events have zero probability—no events outside the sample space are possible as it is the universe of possibilities under consideration, and that the probability of either of two mutually exclusive events occurring is equal to the sum of their individual probabilities.
Bayes' theorem
The probability of an event E conditioned on evidence X is proportional to the prior probability of the event and the likelihood of the evidence given that the event has occurred. This is Bayes' Theorem:

P(X) is the normalizing constant, which is also...























































