Different ML approaches
As we have seen, the term ML is used in a very general way and refers to the general techniques that are used to extrapolate patterns from large sets, or it is the ability to make predictions on new data based on what is learned by analyzing available known data. ML techniques can roughly be divided into two core classes, while one more class is often added. Here are the classes:
- Supervised learning
- Unsupervised learning
- Reinforcement learning
Let’s take a closer look.
Supervised learning
Supervised learning algorithms are a class of ML algorithms that use previously labeled data to learn its features, so they can classify similar but unlabeled data. Let’s use an example to understand this concept better.
Let’s assume that a user receives many emails every day, some of which are important business emails and some of which are unsolicited junk emails, also known as spam. A supervised machine algorithm will be presented with a large body of emails that have already been labeled by a teacher as spam or not spam (this is called training data). For each sample, the machine will try to predict whether the email is spam or not, and it will compare the prediction with the original target label. If the prediction differs from the target, the machine will adjust its internal parameters in such a way that the next time it encounters this sample, it will classify it correctly. Conversely, if the prediction is correct, the parameters will stay the same. The more training data we feed to the algorithm, the better it becomes (this rule has caveats, as we’ll see next).
In the example we used, the emails had only two classes (spam or not spam), but the same principles apply to tasks with arbitrary numbers of classes (or categories). For example, Gmail, the free email service by Google, allows the user to select up to five categories, which are labeled as follows:
- Primary: Includes person-to-person conversations
- Promotions: Includes marketing emails, offers, and discounts
- Social: Includes messages from social networks and media-sharing sites
- Updates: Includes bills, bank statements, and receipts
- Forums: Includes messages from online groups and mailing lists
To summarize, the ML task, which maps a set of input values to a finite number of classes, is called classification.
In some cases, the outcome may not necessarily be discrete, and we may not have a finite number of classes to classify our data into. For example, we may try to predict the life expectancy of a group of people based on their predetermined health parameters. In this case, the outcome is a numerical value, and we don’t talk about classification but rather regression.
One way to think of supervised learning is to imagine we are building a function, f, defined over a dataset, which comprises information organized by features. In the case of email classification, the features can be specific words that may appear more frequently than others in spam emails. The use of explicit sex-related words will most likely identify a spam email rather than a business/work email. On the contrary, words such as meeting, business, or presentation are more likely to describe a work email. If we have access to metadata, we may also use the sender’s information as a feature. Each email will then have an associated set of features, and each feature will have a value (in this case, how many times the specific word is present in the email’s body). The ML algorithm will then seek to map those values to a discrete range that represents the set of classes, or a real value in the case of regression. The definition of the f function is as follows:
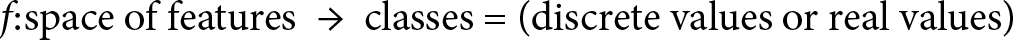
In later chapters, we’ll see several examples of either classification or regression problems. One such problem we’ll discuss is classifying handwritten digits of the Modified National Institute of Standards and Technology (MNIST) database (http://yann.lecun.com/exdb/mnist/). When given a set of images representing 0 to 9, the ML algorithm will try to classify each image in one of the 10 classes, wherein each class corresponds to one of the 10 digits. Each image is 28×28 (= 784) pixels in size. If we think of each pixel as one feature, then the algorithm will use a 784-dimensional feature space to classify the digits.
The following figure depicts the handwritten digits from the MNIST dataset:

Figure 1.1 – An example of handwritten digits from the MNIST dataset
In the next sections, we’ll talk about some of the most popular classical supervised algorithms. The following is by no means an exhaustive list or a thorough description of each ML method. We recommend referring to the book Python Machine Learning, by Sebastian Raschka (https://www.packtpub.com/product/python-machine-learning-third-edition/9781789955750). It’s a simple review meant to provide you with a flavor of the different ML techniques in Python.
Linear and logistic regression
A regression algorithm is a type of supervised algorithm that uses features of the input data to predict a numeric value, such as the cost of a house, given certain features, such as size, age, number of bathrooms, number of floors, and location. Regression analysis tries to find the value of the parameters for the function that best fits an input dataset.
In a linear regression algorithm, the goal is to minimize a cost function by finding appropriate parameters for the function over the input data that best approximates the target values. A cost function is a function of the error – that is, how far we are from getting a correct result. A popular cost function is the mean squared error (MSE), where we take the square of the difference between the expected value and the predicted result. The sum of all the input examples gives us the error of the algorithm and represents the cost function.
Say we have a 100-square-meter house that was built 25 years ago with three bathrooms and two floors. Let’s also assume that the city is divided into 10 different neighborhoods, which we’ll denote with integers from 1 to 10, and say this house is located in the area denoted by 7. We can parameterize this house with a five-dimensional vector,  . Say that we also know that this house has an estimated value of $100,000 (in today’s world, this would be enough for just a tiny shack near the North Pole, but let’s pretend). What we want is to create a function, f, such that
. Say that we also know that this house has an estimated value of $100,000 (in today’s world, this would be enough for just a tiny shack near the North Pole, but let’s pretend). What we want is to create a function, f, such that  .
.
A note of encouragement
Don’t worry If you don’t fully understand some of the terms in this section. We’ll discuss vectors, cost functions, linear regression, and gradient descent in more detail in Chapter 2. We will also see that training NNs and linear/logistic regressions have a lot in common. For now, you can think of a vector as an array. We’ll denote vectors with boldface font – for example,  . We’ll denote the vector elements with italic font and subscript – for example,
. We’ll denote the vector elements with italic font and subscript – for example,  .
.
In linear regression, this means finding a vector of weights,  , such that the dot product of the vectors,
, such that the dot product of the vectors,  , would be
, would be  or
or  . If we had 1,000 houses, we could repeat the same process for every house, and ideally, we would like to find a single vector, w, that can predict the correct value that is close enough for every house. The most common way to train a linear regression model can be seen in the following pseudocode block:
. If we had 1,000 houses, we could repeat the same process for every house, and ideally, we would like to find a single vector, w, that can predict the correct value that is close enough for every house. The most common way to train a linear regression model can be seen in the following pseudocode block:
Initialize the vector w with some random values
repeat:
E = 0 # initialize the cost function E with 0
for every pair  of the training set:
of the training set:
 # here
# here  is the real house price
is the real house price
 # Mean Square Error
use gradient descent to update the weights w based on MSE until MSE falls below threshold
# Mean Square Error
use gradient descent to update the weights w based on MSE until MSE falls below threshold
First, we iterate over the training data to compute the cost function, MSE. Once we know the value of MSE, we’ll use the gradient descent algorithm to update the weights of the vector, w. To do this, we’ll calculate the derivatives of the cost function concerning each weight,  . In this way, we’ll know how the cost function changes (increase or decrease) concerning
. In this way, we’ll know how the cost function changes (increase or decrease) concerning  . Then we’ll update that weight’s value accordingly.
. Then we’ll update that weight’s value accordingly.
Previously, we demonstrated how to solve a regression problem with linear regression. Now, let’s take a classification task: trying to determine whether a house is overvalued or undervalued. In this case, the target data would be categorical [1, 0] – 1 for overvalued and 0 for undervalued. The price of the house will be an input parameter instead of the target value as before. To solve the task, we’ll use logistic regression. This is similar to linear regression but with one difference: in linear regression, the output is  . However, here, the output will be a special logistic function (https://en.wikipedia.org/wiki/Logistic_function),
. However, here, the output will be a special logistic function (https://en.wikipedia.org/wiki/Logistic_function),  . This will squash the value of
. This will squash the value of  in the (0:1) interval. You can think of the logistic function as a probability, and the closer the result is to 1, the more chance there is that the house is overvalued, and vice versa. Training is the same as with linear regression, but the output of the function is in the (0:1) interval, and the labels are either 0 or 1.
in the (0:1) interval. You can think of the logistic function as a probability, and the closer the result is to 1, the more chance there is that the house is overvalued, and vice versa. Training is the same as with linear regression, but the output of the function is in the (0:1) interval, and the labels are either 0 or 1.
Logistic regression is not a classification algorithm, but we can turn it into one. We just have to introduce a rule that determines the class based on the logistic function’s output. For example, we can say that a house is overvalued if the value of  and undervalued otherwise.
and undervalued otherwise.
Multivariate regression
The regression examples in this section have a single numerical output. A regression analysis can have more than one output. We’ll refer to such analysis as multivariate regression.
Support vector machines
A support vector machine (SVM) is a supervised ML algorithm that’s mainly used for classification. It is the most popular member of the kernel method class of algorithms. An SVM tries to find a hyperplane, which separates the samples in the dataset.
Hyperplanes
A hyperplane is a plane in a high-dimensional space. For example, a hyperplane in a one-dimensional space is a point, and in a two-dimensional space, it would just be a line. In three-dimensional space, the hyperplane would be a plane, and we can’t visualize the hyperplane in four-dimensional space, but we know that it exists.
We can think of classification as the process of trying to find a hyperplane that will separate different groups of data points. Once we have defined our features, every sample (in our case, an email) in the dataset can be thought of as a point in the multidimensional space of features. One dimension of that space represents all the possible values of one feature. The coordinates of a point (a sample) are the specific values of each feature for that sample. The ML algorithm task will be to draw a hyperplane to separate points with different classes. In our case, the hyperplane would separate spam from non-spam emails.
In the following diagram, at the top and bottom, we can see two classes of points (red and blue) that are in a two-dimensional feature space (the x and y axes). If both the x and y values of a point are below 5, then the point is blue. In all other cases, the point is red. In this case, the classes are linearly separable, meaning we can separate them with a hyperplane. Conversely, the classes in the image on the right are linearly inseparable:

Figure 1.2 – A linearly separable set of points (left) and a linearly inseparable set (right)
The SVM tries to find a hyperplane that maximizes the distance between itself and the points. In other words, from all possible hyperplanes that can separate the samples, the SVM finds the one that has the maximum distance from all points. In addition, SVMs can deal with data that is not linearly separable. There are two methods for this: introducing soft margins or using the kernel trick.
Soft margins work by allowing a few misclassified elements while retaining the most predictive ability of the algorithm. In practice, it’s better not to overfit the ML model, and we could do so by relaxing some of the SVM hypotheses.
The kernel trick solves the same problem differently. Imagine that we have a two-dimensional feature space, but the classes are linearly inseparable. The kernel trick uses a kernel function that transforms the data by adding more dimensions to it. In our case, after the transformation, the data will be three-dimensional. The linearly inseparable classes in the two-dimensional space will become linearly separable in the three dimensions and our problem is solved:

Figure 1.3 – A non-linearly separable set before the kernel was applied (left) and the same dataset after the kernel has been applied, and the data can be linearly separated (right)
Lets move to the last one in our list, decision trees.
Decision trees
Another popular supervised algorithm is the decision tree, which creates a classifier in the form of a tree. It is composed of decision nodes, where tests on specific attributes are performed, and leaf nodes, which indicate the value of the target attribute. To classify a new sample, we start at the root of the tree and navigate down the nodes until we reach a leaf.
A classic application of this algorithm is the Iris flower dataset (http://archive.ics.uci.edu/ml/datasets/Iris), which contains data from 50 samples of three types of irises
(Iris Setosa, Iris Virginica, and Iris Versicolor). Ronald Fisher, who created the dataset, measured four different features of these flowers:
- The length of their sepals
- The width of their sepals
- The length of their petals
- The width of their petals
Based on the different combinations of these features, it’s possible to create a decision tree to decide which species each flower belongs to. In the following diagram, we have defined a decision tree that will correctly classify almost all the flowers using only two of these features, the petal length and width:

Figure 1.4 – A decision tree for classifying the Iris dataset
To classify a new sample, we start at the root note of the tree (petal length). If the sample satisfies the condition, we go left to the leaf, representing the Iris Setosa class. If not, we go right to a new node (petal width). This process continues until we reach a leaf.
In recent years, decision trees have seen two major improvements. The first is random forests, which is an ensemble method that combines the predictions of multiple trees. The second is a class of algorithms called gradient boosting, which creates multiple sequential decision trees, where each tree tries to improve the errors made by the previous tree. Thanks to these improvements, decision trees have become very popular when working with certain types of data. For example, they are one of the most popular algorithms used in Kaggle competitions.
Unsupervised learning
The second class of ML algorithms is unsupervised learning. Here, we don’t label the data beforehand; instead, we let the algorithm come to its conclusion. One of the advantages of unsupervised learning algorithms over supervised ones is that we don’t need labeled data. Producing labels for supervised algorithms can be costly and slow. One way to solve this issue is to modify the supervised algorithm so that it uses less labeled data; there are different techniques for this. But another approach is to use an algorithm, which doesn’t need labels in the first place. In this section, we’ll discuss some of these unsupervised algorithms.
Clustering
One of the most common, and perhaps simplest, examples of unsupervised learning is clustering. This is a technique that attempts to separate the data into subsets.
To illustrate this, let’s view the spam-or-not-spam email classification as an unsupervised learning problem. In the supervised case, for each email, we had a set of features and a label (spam or not spam). Here, we’ll use the same set of features, but the emails will not be labeled. Instead, we’ll ask the algorithm, when given the set of features, to put each sample in one of two separate groups (or clusters). Then, the algorithm will try to combine the samples in such a way that the intraclass similarity (which is the similarity between samples in the same cluster) is high and the similarity between different clusters is low. Different clustering algorithms use different metrics to measure similarity. For some more advanced algorithms, you don’t have to specify the number of clusters.
The following graph shows how a set of points can be classified to form three subsets:

Figure 1.5 – Clustering a set of points in three subsets
K-means
K-means is a clustering algorithm that groups the elements of a dataset into k distinct clusters (hence the k in the name). Here’s how it works:
- Choose k random points, called centroids, from the feature space, which will represent the center of each of the k clusters.
- Assign each sample of the dataset (that is, each point in the feature space) to the cluster with the closest centroid.
- For each cluster, we recomputed new centroids by taking the mean values of all the points in the cluster.
- With the new centroids, we repeat Steps 2 and 3 until the stopping criteria are met.
The preceding method is sensitive to the initial choice of random centroids, and it may be a good idea to repeat it with different initial choices. It’s also possible for some centroids to not be close to any of the points in the dataset, reducing the number of clusters down from k. Finally, it’s worth mentioning that if we used k-means with k=3 on the Iris dataset, we may get different distributions of the samples compared to the distribution of the decision tree that we’d introduced. Once more, this highlights how important it is to carefully choose and use the correct ML method for each problem.
Now, let’s discuss a practical example that uses k-means clustering. Let’s say a pizza delivery place wants to open four new franchises in a city, and they need to choose the locations for the sites. We can solve this problem with k-means:
- Find the locations where pizza is ordered most often; these will be our data points.
- Choose four random points where the sites will be located.
- By using k-means clustering, we can identify the four best locations that minimize the distance to each delivery place:

Figure 1.6 – The distribution of points where pizza is delivered most often (left); the round points indicate where the new franchises should be located and their corresponding delivery areas (right)
Self-supervised learning
Self-supervised learning refers to a combination of problems and datasets, which allow us to automatically generate (that is, without human intervention) labeled data from the dataset. Once we have these labels, we can train a supervised algorithm to solve our task. To understand this concept better, let’s discuss some use cases:
- Time series forecasting: Imagine that we have to predict the future value of a time series based on its most recent historical values. Examples of this include stock (and nowadays crypto) price prediction and weather forecasting. To generate a labeled data sample, let’s take a window with length k of the historical data that ends at past moment t. We’ll take the historical values in the range [t – k; t] and we’ll use them as input for the supervised algorithm. We’ll also take the historical value at moment t + 1 and we’ll use it as the label for the given input sample. We can apply this division to the rest of the historical values and generate a labeled training dataset automatically.
- Natural language processing (NLP): Similar to time series, the natural text represents a sequence of words (or tokens). We can train an NLP algorithm to predict the next word based on the preceding k words in a similar manner to a time series. However, the natural text does not carry the same strict past/future division as time series do. Because of this, we can use the whole context around the target word as input – that is, words that come both before and after the target word in the consequence, instead of the preceding words only. As we’ll see in Chapter 6, this technique is foundational to contemporary NLP algorithms.
- Autoencoders: This is a special type of NN that tries to reproduce its input. In other words, the target value (label) of an autoencoder is equal to the input data,
 , where i is the sample index. We can formally say that it tries to learn an identity function (a function that repeats its input). Since our labels are just input data, the autoencoder is an unsupervised algorithm. You might be wondering what the point of an algorithm that tries to predict its input is. The autoencoder is split into two parts – an encoder and a decoder. First, the encoder tries to compress the input data into a vector with a smaller size than the input itself. Next, the decoder tries to reproduce the original input based on this smaller internal state vector. By setting this limitation, the autoencoder is forced to extract only the most significant features of the input data. The goal of the autoencoder is to learn a representation of the data that is more efficient or compact than the original representation, while still retaining as much of the original information as possible.
, where i is the sample index. We can formally say that it tries to learn an identity function (a function that repeats its input). Since our labels are just input data, the autoencoder is an unsupervised algorithm. You might be wondering what the point of an algorithm that tries to predict its input is. The autoencoder is split into two parts – an encoder and a decoder. First, the encoder tries to compress the input data into a vector with a smaller size than the input itself. Next, the decoder tries to reproduce the original input based on this smaller internal state vector. By setting this limitation, the autoencoder is forced to extract only the most significant features of the input data. The goal of the autoencoder is to learn a representation of the data that is more efficient or compact than the original representation, while still retaining as much of the original information as possible.
Another interesting application of self-supervised learning is in generative models, as opposed to discriminative models. Let’s discuss the difference between the two. Given input data, a discriminative model will map it to a certain label (in other words, classification or regression). A typical example is the classification of MNIST images in 1 of 10-digit classes, where the NN maps input data features (pixel intensities) to the digit label. We can also say this in another way: a discriminative model gives us the probability of y (class), given x (input) –  . In the case of MNIST, this is the probability of the digit when given the pixel intensities of the image.
. In the case of MNIST, this is the probability of the digit when given the pixel intensities of the image.
On the other hand, a generative model learns how classes are distributed. You can think of it as the opposite of what the discriminative model does. Instead of predicting the class probability, y, given certain input features, it tries to predict the probability of the input features when given a class, y – 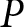
 . For example, a generative model will be able to create an image of a handwritten digit when given the digit class. Since we only have 10 classes, it will be able to generate just 10 images. However, we’ve only used this example to illustrate this concept. In reality, the class could be an arbitrary tensor of values, and the model would be able to generate an unlimited number of images with different features. If you don’t understand this now, don’t worry; we’ll discuss this topic again in Chapter 5. In Chapter 8 and Chapter 9, we’ll discuss how transformers (a new type of NN) have been used to produce some impressive generative models. They have gained popularity both in the research community and the mainstream public because of the attractive results they produce. Two of the most popular visual models are Stable Diffusion (https://github.com/CompVis/stable-diffusion), by Stability AI (https://stability.ai/), and DALL-E (https://openai.com/dall-e-2/), by OpenAI, which can create photorealistic or artistic images from a natural language description. When prompted with the text Musician frog playing on a guitar, Stable Diffusion produces the following figure:
. For example, a generative model will be able to create an image of a handwritten digit when given the digit class. Since we only have 10 classes, it will be able to generate just 10 images. However, we’ve only used this example to illustrate this concept. In reality, the class could be an arbitrary tensor of values, and the model would be able to generate an unlimited number of images with different features. If you don’t understand this now, don’t worry; we’ll discuss this topic again in Chapter 5. In Chapter 8 and Chapter 9, we’ll discuss how transformers (a new type of NN) have been used to produce some impressive generative models. They have gained popularity both in the research community and the mainstream public because of the attractive results they produce. Two of the most popular visual models are Stable Diffusion (https://github.com/CompVis/stable-diffusion), by Stability AI (https://stability.ai/), and DALL-E (https://openai.com/dall-e-2/), by OpenAI, which can create photorealistic or artistic images from a natural language description. When prompted with the text Musician frog playing on a guitar, Stable Diffusion produces the following figure:

Figure 1.7 – Stable Diffusion output for the prompt Musician frog playing on a guitar
Another interesting generative model is OpenAI’s ChatGPT (GPT stands for Generative Pre-trained Transformer), which (as its name suggests) acts as a smart chatbot. ChatGPT can answer follow-up questions, admit mistakes, challenge incorrect premises, and reject inappropriate requests.
Reinforcement learning
The third class of ML techniques is called reinforcement learning (RL). We will illustrate this with one of the most popular applications of RL: teaching machines how to play games. The machine (or agent) interacts with the game (or environment). The goal of the agent is to win the game. To do this, the agent takes actions that can change the environment’s state. The environment reacts to the agent’s actions and provides it with reward (or penalty) signals that help the agent to decide its next action. Winning the game would provide the biggest reward. In formal terms, the goal of the agent is to maximize the total rewards it receives throughout the game:

Figure 1.8 – The interaction between different elements of an RL system
Let’s imagine a game of chess as an RL problem. Here, the environment would include the chessboard, along with the locations of the pieces. The goal of our agent is to beat the opponent. The agent will then receive a reward when they capture the opponent’s piece, and they will win the biggest reward if they checkmate the opponent. Conversely, if the opponent captures a piece or checkmates the agent, the reward will be negative. However, as part of their larger strategies, the players will have to make moves that neither capture a piece nor checkmate the other’s king. The agent won’t receive any reward then. If this was a supervised learning problem, we would have to provide a label or a reward for each move. This is not the case with RL. In the RL framework, the agent will improvise with a trial-and-error approach to decide its next actions.
Let’s take another example, in which sometimes we have to sacrifice a pawn to achieve a more important goal (such as a better position on the chessboard). In such situations, our humble agent has to be smart enough to take a short-term loss as a long-term gain. In an even more extreme case, imagine we had the bad luck of playing against Ding Liren, the current world chess champion. Surely, the agent will lose in this case. However, how would we know which moves were wrong and led to the agent’s loss? Chess belongs to a class of problems where the game should be considered in its entirety to reach a successful solution, rather than just looking at the immediate consequences of each action. RL will give us the framework that will help the agent to navigate and learn in this complex environment.
An interesting problem arises from this newfound freedom to take action. Imagine that the agent has learned one successful chess-playing strategy (or policy, in RL terms). After some games, the opponent might guess what that policy is and manage to beat us. The agent will now face a dilemma with the following decisions: either to follow the current policy and risk becoming predictable, or to experiment with new moves that will surprise the opponent, but also carry the risk of turning out even worse. In general terms, the agent uses a policy that gives them a certain reward, but their ultimate goal is to maximize the total reward. A modified policy might be more rewarding, and the agent will be ineffective if they don’t try to find such a policy. One of the challenges of RL is the trade-off between exploitation (following the current policy) and exploration (trying new moves).
So far, we’ve used only games as examples; however, many problems can fall into the RL domain. For example, you can think of autonomous vehicle driving as an RL problem. The vehicle can get positive rewards if it stays within its lane and observes the traffic rules. It will gain negative rewards if it crashes. Another interesting recent application of RL is in managing stock portfolios. The goal of the agent would be to maximize the portfolio value. The reward is directly derived from the value of the stocks in the portfolio.
On the absence of RL in this edition
The second edition of this book had two chapters on RL. In this edition, we’ll omit those chapters, and we’ll discuss transformers and their applications instead. On one hand, RL is a promising field, but at present, training RL models is slow, and their practical applications are limited. Because of this, RL research is mostly concentrated in well-funded commercial companies and academic institutions. On the other hand, transformers have represented the next big step in the field of ML, in the same way as GPU-trained deep networks sparked interest in the field in the 2009-2012 period.
Q-learning
Q-learning is an off-policy temporal-difference RL algorithm. What a mouthful! But fear not; let’s not worry about what all this means, and instead just see how the algorithm works. To do this, we’ll use the game of chess we introduced in the previous section. As a reminder, the board’s configuration (the locations of the pieces) is the current state of the environment. Here, the agents can take actions, a, by moving pieces, thus changing the state into a new one. We’ll represent a game of chess as a graph where the different board configurations are the graph’s vertices, and the possible moves from each configuration are the edges. To make a move, the agent follows the edge from the current state, s, to a new state, s’. The basic Q-learning algorithm uses a Q-table to help the agent decide which moves to make. The Q-table contains one row for each board configuration, while the columns of the table are all possible actions that the agent can take (the moves). A table cell, q(s, a), contains the cumulative expected reward, called a Q-value. This is the potential total reward that the agent will receive for the remainder of the game if they take an action, a, from their current state, s. At the beginning, the Q-table is initialized with an arbitrary value. With that knowledge, let’s see how Q-learning works:
Initialize the Q table with some arbitrary value
for each episode:
Observe the initial state s
for each step of the episode:
Select new action a using Q-table based policy
Observe reward r and go to the new state s'
Use Bellman eq to update q(s, a) in the Q-table
until we reach a terminal state for the episode
An episode starts with a random initial state and finishes when we reach the terminal state. In our case, one episode would be one full game of chess.
The question that arises is, how does the agent’s policy determine what will be the next action? To do so, the policy has to consider the Q-values of all the possible actions from the current state. The higher the Q-value, the more attractive the action is. However, the policy will sometimes ignore the Q-table (exploitation of the existing knowledge) and choose another random action to find higher potential rewards (exploration). In the beginning, the agent will take random actions because the Q-table doesn’t contain much information (a trial-and-error approach). As time progresses and the Q-table is gradually filled, the agent will become more informed in interacting with the environment.
We update q(s, a) after each new action by using the Bellman equation. The Bellman equation is beyond the scope of this introduction, but it’s enough to know that the updated value, q(s, a), is based on the newly received reward, r, as well as the maximum possible Q-value, q*(s’, a’), of the new state, s’.
This example was intended to help you understand the basic workings of Q-learning, but you might have noticed an issue with this. We store the combination of all possible board configurations and moves in the Q-table. This would make the table huge and impossible to fit in today’s computer memory. Fortunately, there is a solution for this: we can replace the Q-table with an NN, which will tell the agent what the optimal action is in each state. In recent years, this development has allowed RL algorithms to achieve superhuman performance on tasks such as the games of Go, Dota 2, Doom, and StarCraft.
Components of an ML solution
So far, we’ve discussed three major classes of ML algorithms. However, to solve an ML problem, we’ll need a system in which the ML algorithm is only part of it. The most important aspects of such a system are as follows:
- Learner: This algorithm is used with its learning philosophy. The choice of this algorithm is determined by the problem we’re trying to solve since different problems can be better suited for certain ML algorithms.
- Training data: This is the raw dataset that we are interested in. This can be labeled or unlabeled. It’s important to have enough sample data for the learner to understand the structure of the problem.
- Representation: This is how we express the data in terms of the chosen features so that we can feed it to the learner. For example, to classify handwritten images of digits, we’ll represent the image as a two-dimensional array of values, where each cell will contain the color value of one pixel. A good choice of representation of the data is important for achieving better results.
- Goal: This represents the reason to learn from the data for the problem at hand. This is strictly related to the target and helps us define how and what the learner should use and what representation to use. For example, the goal may be to clean our mailboxes of unwanted emails, and this goal defines what the target of our learner is. In this case, it is the detection of spam emails.
- Target: This represents what is being learned as well as the final output. The target can be a classification of unlabeled data, a representation of input data according to hidden patterns or characteristics, a simulator for future predictions, or a response to an outside stimulus or strategy (in the case of RL).
It can never be emphasized enough: any ML algorithm can only achieve an approximation of the target and not a perfect numerical description. ML algorithms are not exact mathematical solutions to problems – they are just approximations. In the Supervised learning section, we defined learning as a function from the space of features (the input) into a range of classes. Later, we’ll see how certain ML algorithms, such as NNs, can approximate any function to any degree, in theory. This is called the universal approximation theorem (https://en.wikipedia.org/wiki/Universal_approximation_theorem), but it does not imply that we can get a precise solution to our problem. In addition, solutions to the problem can be better achieved by better understanding the training data.
Typically, a problem that can be solved with classic ML techniques may require a thorough understanding and processing of the training data before deployment. The steps to solve an ML problem are as follows:
- Data collection: This involves gathering as much data as possible. In the case of supervised learning, this also includes correct labeling.
- Data processing: This involves cleaning the data, such as removing redundant or highly correlated features, or even filling in missing data, and understanding the features that define the training data.
- Creation of the test case: Usually, the data can be divided into three sets:
- Training set: We use this set to train the ML algorithm. In most cases, we’ll train the algorithm by iterating the whole training set more than once. We’ll refer to the number of full training set iterations as epochs.
- Validation set: We use this set to evaluate the accuracy of the algorithm with unknown data during training. We’ll train the algorithm for some time on the training set and then we’ll use the validation set to check its performance. If we are not satisfied with the result, we can tune the hyperparameters of the algorithm and repeat the process. The validation set can also help us determine when to stop the training. We’ll learn more about this later in this section.
- Test set: When we finish tuning the algorithm with the training or validation cycle, we’ll use the test set only once for a final evaluation. The test set is similar to the validation set in the sense that the algorithm hasn’t used it during training. However, when we strive to improve the algorithm on the validation data, we may inadvertently introduce bias, which can skew the results in favor of the validation set and not reflect the actual performance. Because we use the test only once, this will provide a more objective measurement of the algorithm.
Note
One of the reasons for the success of DL algorithms is that they usually require less data processing than classic methods. For a classic algorithm, you would have to apply different data processing and extract different features for each problem. With DL, you can apply the same data processing pipeline for most tasks. With DL, you can be more productive, and you don’t need as much domain knowledge for the task at hand compared to the classic ML algorithms.
There are many valid reasons to create testing and validation datasets. As mentioned previously, ML techniques can only produce an approximation of the desired result. Often, we can only include a finite and limited number of variables, and there may be many variables that are outside of our control. If we only used a single dataset, our model may end up memorizing the data and producing an extremely high accuracy value on the data it has memorized. However, this result may not be reproducible on other similar but unknown datasets. One of the key goals of ML algorithms is their ability to generalize. This is why we create both a validation set used for tuning our model selection during training and a final test set only used at the end of the process to confirm the validity of the selected algorithm.
To understand the importance of selecting valid features and to avoid memorizing the data, which is also referred to as overfitting in the literature (we’ll use this term from now on), let’s use a joke taken from an XKND comic as an example (http://xkcd.com/1122):
It’s apparent that such a rule is meaningless, but it underscores the importance of selecting valid features, and how the question, “How much is a name worth in Scrabble?” can bear any relevance while selecting a US president. Also, this example doesn’t have any predictive power over unknown data. We’ll call this overfitting, which refers to making predictions that fit the data at hand perfectly but don’t generalize to larger datasets. Overfitting is the process of trying to make sense of what we’ll call noise (information that does not have any real meaning) and trying to fit the model to small perturbations.
To explain this further, let’s try to use ML to predict the trajectory of a ball thrown from the ground up into the air (not perpendicularly) until it reaches the ground again. Physics teaches us that the trajectory is shaped like a parabola. We also expect that a good ML algorithm observing thousands of such throws would come up with a parabola as a solution. However, if we were to zoom into the ball and observe the smallest fluctuations in the air due to turbulence, we might notice that the ball does not hold a steady trajectory but may be subject to small perturbations, which in this case is the noise. An ML algorithm that tries to model these small perturbations would fail to see the big picture and produce a result that is not satisfactory. In other words, overfitting is the process that makes the ML algorithm see the trees but forget about the forest:

Figure 1.9 – A good prediction model (left) and a bad (overfitted) prediction model, with the trajectory of a ball thrown from the ground (right)
This is why we separate the training data from the validation and test data; if the algorithm’s accuracy over the test data was not similar to the training data accuracy, that would be a good indication that the model overfits. We need to make sure that we don’t make the opposite error either – that is, underfitting the model. In practice, though, if we aim to make our prediction model as accurate as possible on our training data, underfitting is much less of a risk, and care is taken to avoid overfitting.
The following figure depicts underfitting:

Figure 1.10 – Underfitting can be a problem as well
Neural networks
We introduced some of the popular classical ML algorithms in the previous sections. In this section, we’ll talk about NNs, which are the focus of this book.
The first example of an NN is called the perceptron, and this was invented by Frank Rosenblatt in 1957. The perceptron is a classification algorithm that is very similar to logistic regression. Similar to logistic regression, it has a vector of weights, w, and its output is a function,  , of the dot product,
, of the dot product,  (or
(or  ), of the weights and input.
), of the weights and input.
The only difference is that f is a simple step function – that is, if  , then
, then  , or else
, or else  , wherein we apply a similar logistic regression rule over the output of the logistic function. The perceptron is an example of a simple one-layer neural feedforward network:
, wherein we apply a similar logistic regression rule over the output of the logistic function. The perceptron is an example of a simple one-layer neural feedforward network:

Figure 1.11 – A simple perceptron with three inputs and one output
The perceptron was very promising, but it was soon discovered that it has serious limitations as it only works for linearly separable classes. In 1969, Marvin Minsky and Seymour Paper demonstrated that it could not learn even a simple logical function such as XOR. This led to a significant decline in the interest in perceptrons.
However, other NNs can solve this problem. A classic multilayer perceptron has multiple interconnected perceptrons, such as units that are organized in different sequential layers (input layer, one or more hidden layers, and an output layer). Each unit of a layer is connected to all units of the next layer. First, the information is presented to the input layer, then we use it to compute the output (or activation),  , for each unit of the first hidden layer. We propagate forward, with the output as input for the next layers in the network (hence feedforward), and so on until we reach the output. The most common way to train NNs is by using gradient descent in combination with backpropagation. We’ll discuss this in detail in Chapter 2.
, for each unit of the first hidden layer. We propagate forward, with the output as input for the next layers in the network (hence feedforward), and so on until we reach the output. The most common way to train NNs is by using gradient descent in combination with backpropagation. We’ll discuss this in detail in Chapter 2.
The following diagram depicts an NN with one hidden layer:

Figure 1.12 – An NN with one hidden layer
Think of the hidden layers as an abstract representation of the input data. This is the way the NN understands the features of the data with its internal logic. However, NNs are non-interpretable models. This means that if we observe the  activations of the hidden layer, we wouldn’t be able to understand them. For us, they are just a vector of numerical values. We need the output layer to bridge the gap between the network’s representation and the actual data we’re interested in. You can think of this as a translator; we use it to understand the network’s logic, and at the same time, we can convert it into the actual target values that we are interested in.
activations of the hidden layer, we wouldn’t be able to understand them. For us, they are just a vector of numerical values. We need the output layer to bridge the gap between the network’s representation and the actual data we’re interested in. You can think of this as a translator; we use it to understand the network’s logic, and at the same time, we can convert it into the actual target values that we are interested in.
The universal approximation theorem tells us that a feedforward network with one hidden layer can represent any function. It’s good to know that there are no theoretical limits on networks with one hidden layer, but in practice, we can achieve limited success with such architectures. In Chapter 3, we’ll discuss how to achieve better performance with deep NNs, and their advantages over the shallow ones. For now, let’s apply our knowledge by solving a simple classification task with an NN.
Introducing PyTorch
In this section, we’ll introduce PyTorch – an open source Python DL framework that was developed primarily by Facebook that has been gaining momentum recently. It provides graphics processing unit (GPU) accelerated multidimensional array (or tensor) operations, and computational graphs, which we can use to build NNs. Throughout this book, we’ll use PyTorch and Keras, and we’ll talk about these libraries and compare them in detail in Chapter 3.
Let’s create a simple NN that will classify the Iris flower dataset. The steps are as follows:
- Start by loading the dataset:
import pandas as pd dataset = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data', names=['sepal_length', 'sepal_width', 'petal_length', 'petal_width', 'species']) dataset['species'] = pd.Categorical(dataset['species']).codes dataset = dataset.sample(frac=1, random_state=1234) train_input = dataset.values[:120, :4] train_target = dataset.values[:120, 4] test_input = dataset.values[120:, :4] test_target = dataset.values[120:, 4]The preceding code is boilerplate code that downloads the Iris dataset’s CSV file and then loads it into a pandas DataFrame called
dataset. Then, we shuffle the DataFrame’s rows and split the code into NumPy arrays,train_input/train_target(flower properties/flower class), for the training data andtest_input/test_targetfor the test data. We’ll use 120 samples for training and 30 for testing. If you are not familiar with pandas, think of this as an advanced version of NumPy. - Next, define our first NN. We’ll use a feedforward network with one hidden layer with five units, a ReLU activation function (this is just another type of activation, defined simply as f(x) = max(0, x)), and an output layer with three units. The output layer has three units, and each unit corresponds to one of the three classes of Iris flowers. The following is the PyTorch definition of the network:
import torch torch.manual_seed(1234) hidden_units = 5 net = torch.nn.Sequential( torch.nn.Linear(4, hidden_units), torch.nn.ReLU(), torch.nn.Linear(hidden_units, 3) )
We’ll use one-hot encoding for the target data. This means that each class of the flower will be represented as an array (
Iris Setosa = [1, 0, 0],Iris Versicolor = [0, 1, 0], andIris Virginica = [0, 0, 1]), and one element of the array will be the target for one unit of the output layer. When the network classifies a new sample, we’ll determine the class by taking the unit with the highest activation value.torch.manual_seed(1234)enables us to use the same random data seed every time for the reproducibility of results. - Choose the
lossfunction:criterion = torch.nn.CrossEntropyLoss()
With the
criterionvariable, we define the loss function as cross-entropy loss. The loss function will measure how different the output of the network is compared to the target data. - Define the stochastic gradient descent (SGD) optimizer (a variation of the gradient descent algorithm) with a learning rate of 0.1 and a momentum of 0.9 (we’ll discuss SGD and its parameters in Chapter 2):
optimizer = torch.optim.SGD(net.parameters(), lr=0.1, momentum=0.9)
- Train the network:
epochs = 50 for epoch in range(epochs): inputs = torch.autograd.Variable( torch.Tensor(train_input).float()) targets = torch.autograd.Variable( torch.Tensor(train_target).long()) optimizer.zero_grad() out = net(inputs) loss = criterion(out, targets) loss.backward() optimizer.step() if epoch == 0 or (epoch + 1) % 10 == 0: print('Epoch %d Loss: %.4f' % (epoch + 1, loss.item()))We’ll run the training for 50 epochs, which means that we’ll iterate 50 times over the training dataset:
- Create the
torchvariables from the NumPy array – that is,train_inputandtrain_target. - Zero the gradients of the optimizer to prevent accumulation from the previous iterations. We feed the training data to the NN,
net(inputs), and we compute the loss function’scriterion(out,targets) between the network output and the target data. - Propagate the
lossvalue back through the network. We’re doing this so that we can calculate how each network weight affects the loss function. - The optimizer updates the weights of the network in a way that will reduce the future loss function’s values.
When we run the training, the output will be as follows:
Epoch 1 Loss: 1.2181 Epoch 10 Loss: 0.6745 Epoch 20 Loss: 0.2447 Epoch 30 Loss: 0.1397 Epoch 40 Loss: 0.1001 Epoch 50 Loss: 0.0855
The following graph shows how the loss function decreases with each epoch. This shows how the network gradually learns the training data:
- Create the

Figure 1.13 – The loss function decreases with each epoch
- Let’s see what the final accuracy of our model is:
import numpy as np inputs = torch.autograd.Variable(torch.Tensor(test_input).float()) targets = torch.autograd.Variable(torch.Tensor(test_target).long()) optimizer.zero_grad() out = net(inputs) _, predicted = torch.max(out.data, 1) error_count = test_target.size - np.count_nonzero((targets == predicted).numpy()) print('Errors: %d; Accuracy: %d%%' % (error_count, 100 * torch.sum(targets == predicted) / test_target.size))We do this by feeding the test set to the network and computing the error manually. The output is as follows:
Errors: 0; Accuracy: 100%
We were able to classify all 30 test samples correctly.
We must also try different hyperparameters of the network and see how the accuracy and loss functions work. You could try changing the number of units in the hidden layer, the number of epochs we train in the network, as well as the learning rate.
























































