Dynamic systems modeling
In this section, we will analyze a real case of modeling a production process. In this way, we will learn how to deal with the elements of the system and how to translate the production instances into the elements of the model. A model is created to study the behavior of a system over time. It consists of a set of assumptions about the behavior of the system being expressed using mathematical-logical-symbolic relationships. These relationships are between the entities that make up the system. Recall that a model is used to simulate changes in the system and predict the effects of these changes on the real system. Simple models are resolved analytically using mathematical methods, while complex models are numerically simulated on the computer, where the model results are treated like data from a real system.
Managing workshop machinery
In this section, we will look at a simple example of how a discrete event simulation of a dynamic system is created. A discrete event system is a dynamic system whose states can assume logical or symbolic values, rather than numerical ones, and whose behavior is characterized by the occurrence of instantaneous events within an irregular timing sequence, not necessarily known a priori. The behavior of these systems is described in terms of states and events.
In a workshop, there are two machines that we will call A1 and A2. At the beginning of the day, five jobs need to be carried out: W1, W2, W3, W4, and W5. The following table shows the time (minutes) we need to work on the machines:
|
A1 |
A2 |
|
|
W1 |
30 |
50 |
|
W2 |
0 |
40 |
|
W3 |
20 |
70 |
|
W4 |
30 |
0 |
|
W5 |
50 |
20 |
Table 1.1: Table showing work time on the machines
A zero indicates that a job does not require that machine. Jobs that require two machines must pass through A1 and then through A2. Suppose that we decide to carry out the jobs by assigning them to each machine so that when they become available, the first executable job is started first, in order from 1 to 5. If at the same time, more jobs can be executed on the same machine, we will execute the one with a minor index first.
The purpose of modeling is to determine the minimum time needed to complete all the work. The events in which state changes can occur in the system are as follows:
- A job becomes available for a machine
- A machine starts a job
- A machine ends a job
Based on these rules and the evaluation times indicated in the previous table, we can insert the sequence of the jobs, along with the events scheduled according to the execution times, into a table:
|
Time (minutes) |
A1 |
A2 |
||
|
Start |
End |
Start |
End |
|
|
0 |
W1 |
W2 |
||
|
30 |
W3 |
W1 |
||
|
40 |
W1 |
W2 |
||
|
50 |
W4 |
W3 |
||
|
80 |
W5 |
W4 |
||
|
90 |
W3 |
W1 |
||
|
130 |
W5 |
|||
|
160 |
W5 |
W3 |
||
|
180 |
W5 |
|||
Table 1.2: Table of job sequences
This table shows the times of the events in sequence, indicating the start and end of the work associated with the two machines available in the workshop. At the end of each job, a new job is sent to each machine according to the rules set previously. In this way, the deadlines for the work and the subsequent start of another job are clearly indicated. This is just as easy as it is to identify the time interval in which each machine is used and when it becomes available again. The table solution we have proposed represents a simple and immediate way of simulating a simple dynamic discrete system.
The example we just discussed is a typical case of a dynamic system in which time proceeds in steps in a discrete way. However, many dynamic systems are best described by assuming that time passes continuously. In the next section, we will analyze the case of a continuous dynamic system.
Simple harmonic oscillator
Consider a mass m, resting on a horizontal plane, without friction, and attached to a wall by an ideal spring, of elastic constant k. Suppose that when the horizontal coordinate x is zero, the spring is at rest. The following diagram shows the scheme of a simple harmonic oscillator:
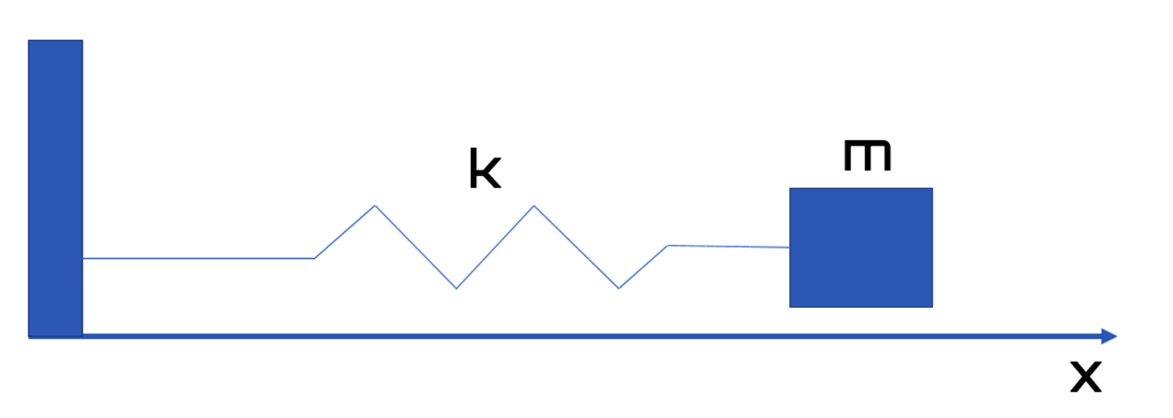
Figure 1.4: The scheme of a harmonic oscillator
If the block of mass m is moved to the right with respect to its equilibrium position (x> 0), the spring being elongated pulls it to the left. Conversely, if the block is placed to the left of its equilibrium position (x < 0), then the spring is compressed and pushes the block to the right. In both cases, we can express the component along the x axis of the force due to the spring according to the following formula:

Here, we have the following:
 is the force
is the force  is the elastic constant
is the elastic constant is the horizontal coordinate that indicates the position of the mass m
is the horizontal coordinate that indicates the position of the mass m
From the second law of dynamics, we can derive the component of acceleration along x as follows:
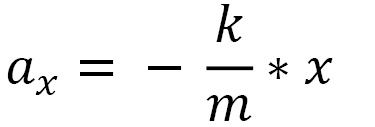
Here, we have the following:
 is the acceleration
is the acceleration  is the elastic constant
is the elastic constant is the mass of the block
is the mass of the block is the horizontal coordinate that indicates the position of the mass m
is the horizontal coordinate that indicates the position of the mass m
If we indicate with  the rate of change of the speed and with
the rate of change of the speed and with  the speed, we can obtain the evolution equations of the dynamic system, as follows:
the speed, we can obtain the evolution equations of the dynamic system, as follows:
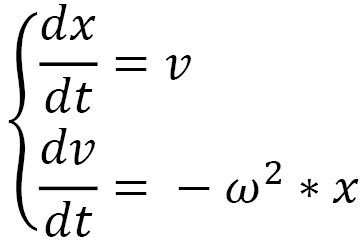
Here, we have the following:
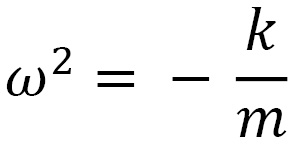
For these equations, we must associate the initial conditions of the system, which we can write in the following way:
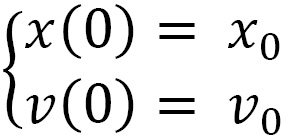
The solutions to the previous differential equations are as follows:
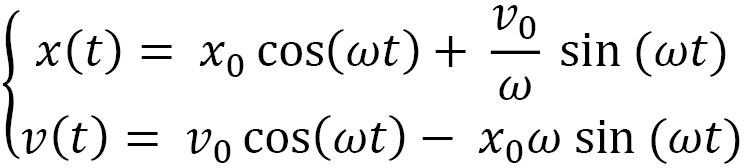
In this way, we obtained the mathematical model of the analyzed system. To study the evolution of the oscillation phenomenon of the mass block m over time, it is enough to vary the time and calculate the position of the mass at that instant and its speed.
In decision-making processes characterized by high levels of complexity, the use of analytical models is not possible. In these cases, it is necessary to resort to models that differ from those of an analytical type for the use of the calculator as a tool not only for calculation, such as in mathematical programming models but also for representing the elements that make up reality while studying the relationships between them.
The predator-prey model
In the field of simulations, simulating the functionality of production and logistic processes is considerably important. These systems are, in fact, characterized by high complexity, numerous interrelationships between the different processes that pass through them, segment failures, unavailability, and the stochasticity of the system parameters.
To understand how complex the analytical modeling of some phenomena is, let’s analyze a universally widespread biological model. This is the predator-prey model, which was developed independently by the Italian researcher Vito Volterra and the American biophysicist Alfred Lotka.
On an island, there are two populations of animals: prey and predators. The vegetation of the island provides the prey with nourishment in quantities that we can consider as unlimited, while the prey is the only food available for predators. We can consider the birth rate of the prey constant over time; this means that in the absence of predators, the prey would grow by exponential law. Their mortality rate, on the other hand, depends on the probability they have of falling prey to a predator and, therefore, on the number of predators present per unit area.
As for predators, the mortality rate is constant, while their growth rate depends on the availability of food and, therefore, on the number of prey per unit area present on the island. We want to study the trend of the size of the two populations over time, starting from a known initial situation (number of prey and predators).
To carry out a simulation of this biological system, we can model it by means of the following system of finite difference equations, where x(t) and y(t) are the numbers of prey and predators at time t, respectively:
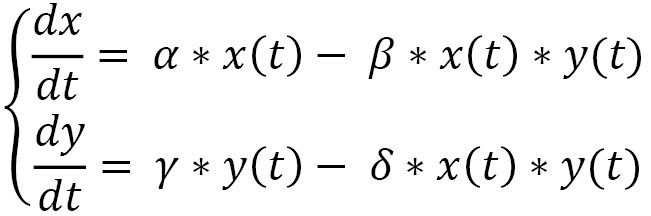
Here, we have the following:
- α, β, γ, δ are positive real parameters related to the interaction of the two species
 is the instantaneous growth rate of the prey
is the instantaneous growth rate of the prey is the instantaneous growth rate of the predators
is the instantaneous growth rate of the predators
The following hypotheses are underlined in this model:
- In the absence of predators, the number of prey increases according to an exponential law, that is, at a constant rate
- Similarly, in the absence of prey, the number of predators decreases at a constant rate
This is a deterministic and continuous simulation model. In fact, the state of the system, represented by the size of the two populations in each instance of time, is univocally determined by the initial state and the parameters of the model. Furthermore, at least in principle, the variables – that is, the size of the populations – vary continuously over time.
The differential system is in normal form and can be solved with respect to the derivatives of maximum order but cannot be separated into variables. It is not possible to solve this in an analytical form, but with numerical methods, it is solved immediately (Runge-Kutta method). The solution obviously depends on the values of the four constants and the initial values.
After analyzing how to model dynamic systems, let’s see step by step how to perform a simulation of a real system.
























































