Exploring vector rotation
Let us start with the most basic rotation we will have in the code, the natural-feeling rotation around the three axes in a three-dimensional cartesian space.
The Euler rotations
In the 18th century, the German mathematician Leonhard Euler (1707-1783) discovered the rule that a composition of two rotations in three-dimensional space is again a rotation, and these rotations differ only by the rotation axis.
We still use this rotation theorem today, to rotate objects around in virtual worlds. The final rotation of a three-dimensional object is a composition of rotations around the x, y, and z axis in three-dimensional cartesian space:
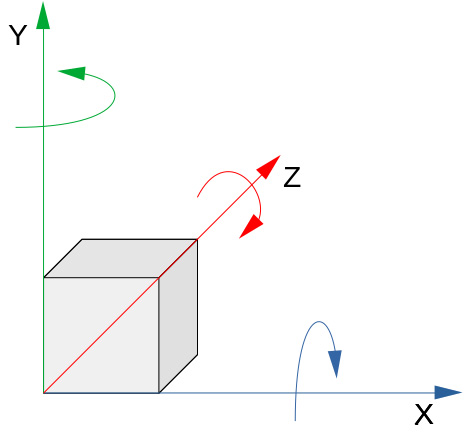
Figure 7.5: The three-dimensional cartesian space, plus the x, y, and z rotation axes
The rotations themselves are defined by the sine and cosine of the rotation angle:
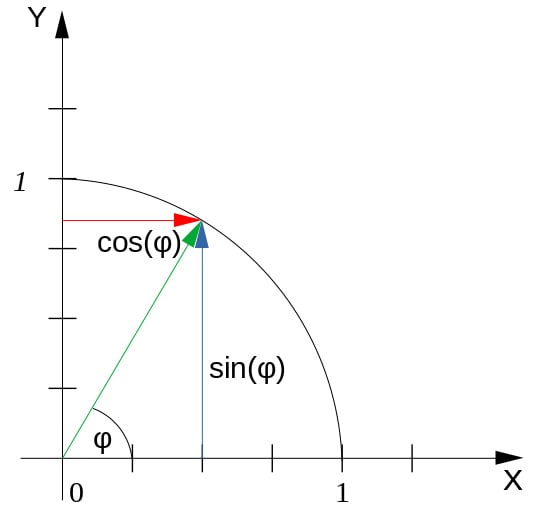
Figure 7.6: Definition of the sine and the cosine of an angle 
We are using the inverse of...























































