Vectors

A long time ago in a country far, far away, there lived an ancient Greek mathematician named Euclid. He wrote a book that defined space using only three dimensions. We will use his vector space to define superposition in quantum computing. Don't be fooled—vector spaces have evolved tremendously since Euclid's days, and our definition of them will evolve too as the book progresses. But for now, we will stick to real numbers, and we'll actually only need two out of the three dimensions Euclid proposed.

To start, we will define a Euclidean vector as being a line segment with a length or magnitude and pointing in a certain direction, as shown in the following screenshot:

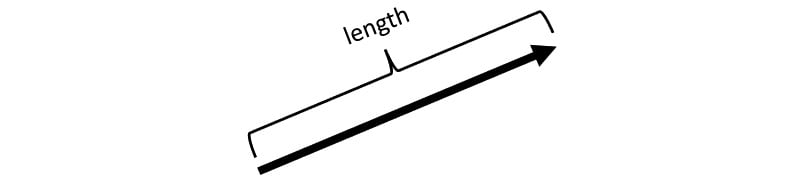
Figure 1.1 – Euclidean vector

Two vectors are equal if they have the same length and direction, so the following vectors are all equal:

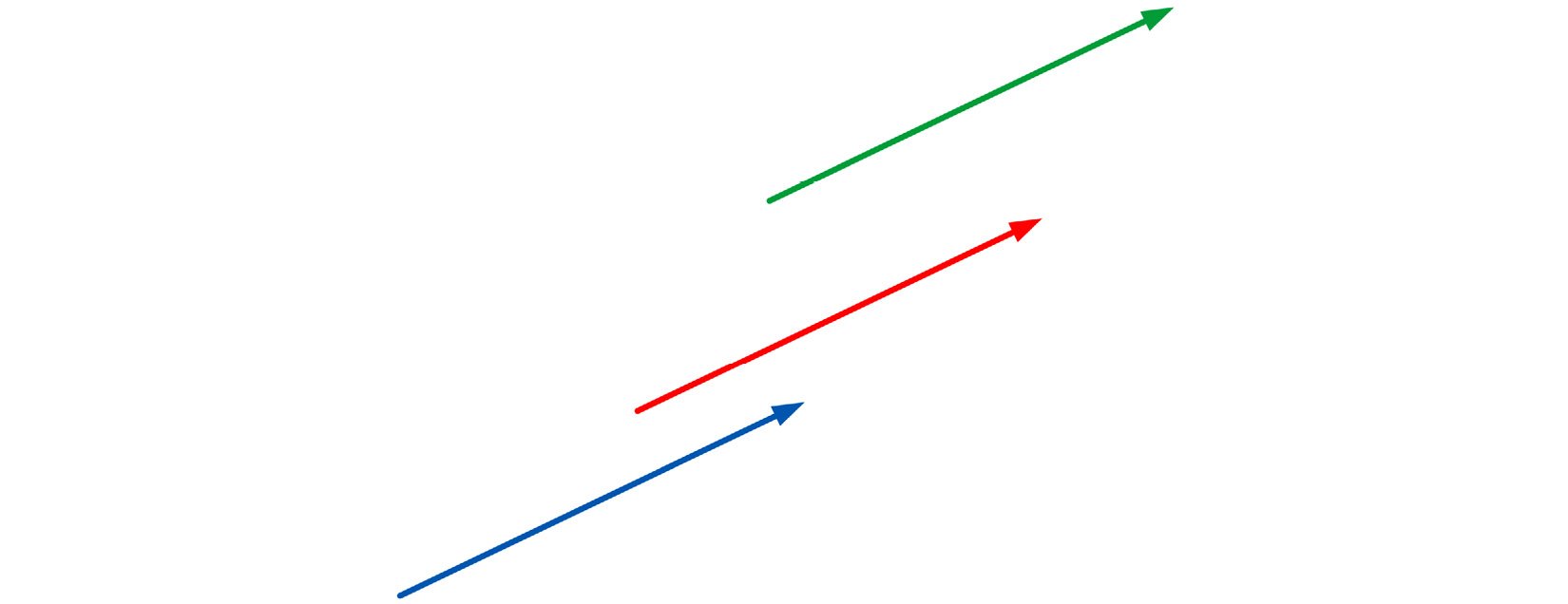
Figure 1.2 – Equal vectors

Vectors can be represented algebraically by their components. The simplest way to do this is to have them start at the origin (the point (0,0)) and use their x and y coordinates, as shown in the following screenshot:

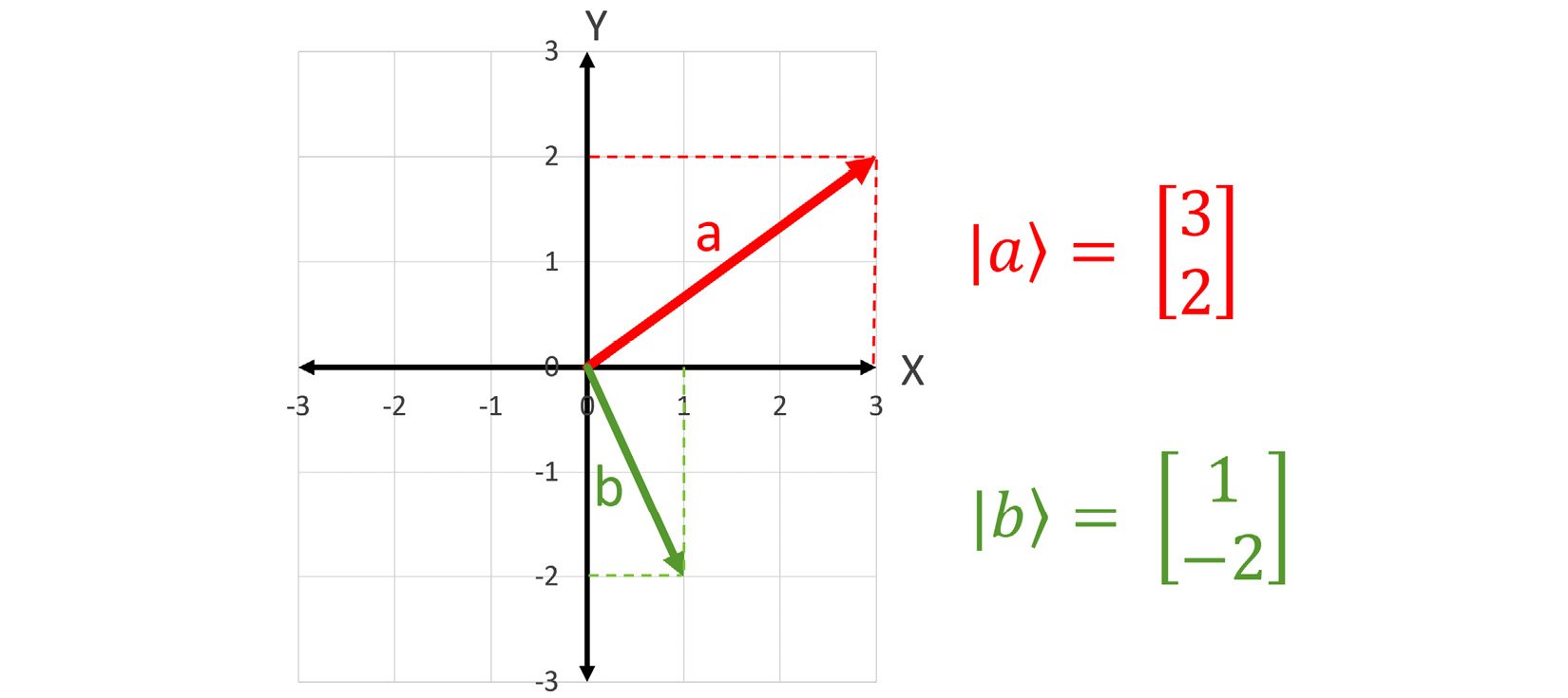
Figure 1.3 – Vectors represented geometrically and algebraically

You should note that I am using a special notation to label the vectors. It is called bra-ket notation. The appendix has more information on this notation, but for now, we will use a vertical bar or pipe, |, followed by the variable name for the vector and then an angle bracket, ⟩, to denote a vector (for example, |a⟩). The coordinates of our vectors will be enclosed in brackets [ ]. The x coordinate will be on top and the y coordinate on the bottom. Vectors are also called "kets" in this notation—for example, ket a, but for now, we will stick with the name vector.

Vector addition

So, it ends up that we can add vectors together both geometrically and algebraically, as shown in the following screenshot:

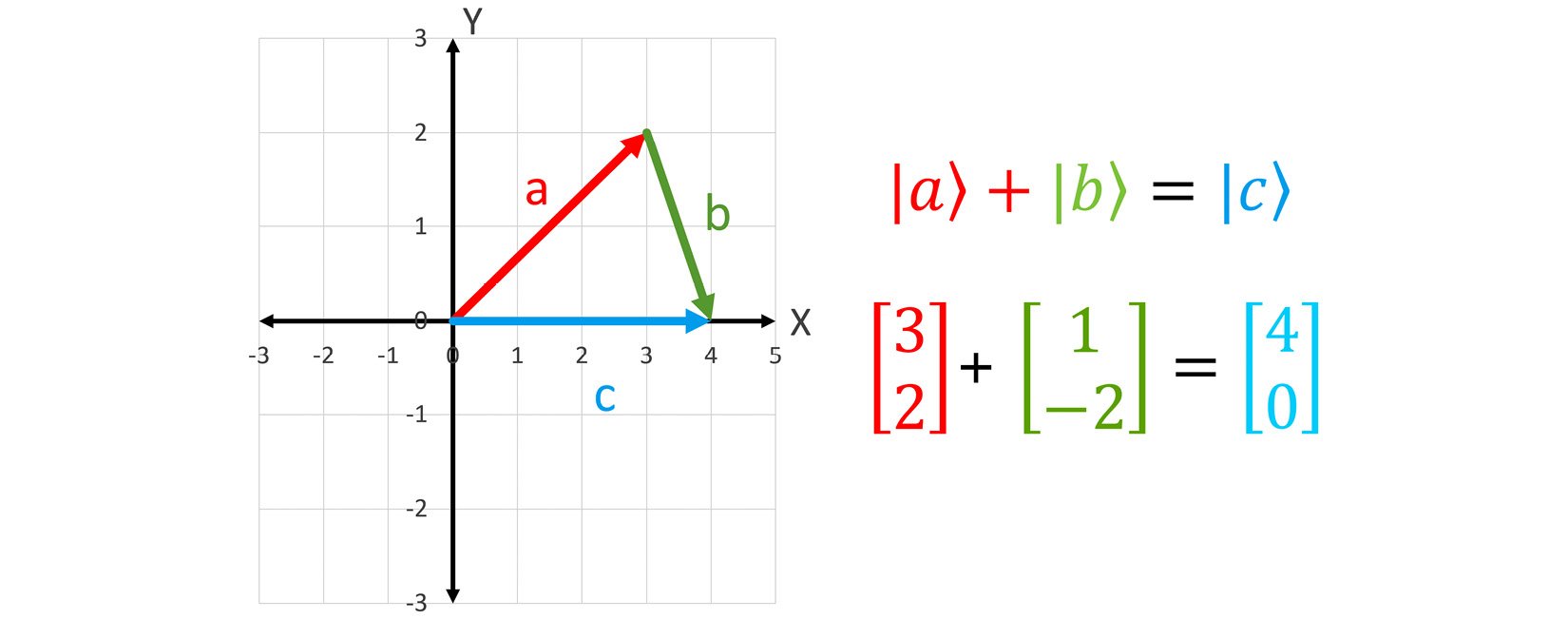
Figure 1.4 – Vector addition

As you can see, we can take vectors and move them in the XY-plane as long as we preserve their length and direction. We have taken the vector |b⟩ from our first graph and moved its start position to the end of vector |a⟩. Once we do that, we can draw a third vector |c⟩ that connects the start of |a⟩ and the end of |b⟩ to form their sum. If we look at the coordinates of |c⟩, it is four units in the x direction and zero units in the y direction. This corresponds to the answer we see on the right of Figure 1.4.

We can also do this addition without the help of a graph, as shown on the right of Figure 1.4. Just adding the first components (3 and 1) gives 4, and adding the second components of the vectors (2 and -2) gives 0. Thus, vector addition works both geometrically and algebraically in two dimensions. So, let's look at an example.

Example

What is the sum of |m⟩ and |n⟩ here?

The solution is:

Exercise 1

Now, you try. The answers are at the end of this chapter:

• What is |m⟩ - |n⟩?
• What is |n⟩ - |m⟩?
• Solve the following expression (notice we use three-dimensional (3D) vectors, but everything works the same):

Scalar multiplication

We can also multiply our vectors by numbers or scalars. They are called scalars because they "scale" a vector, as we will see. The following screenshot shows a vector that is multiplied by a number on the left and the same thing algebraically on the right:

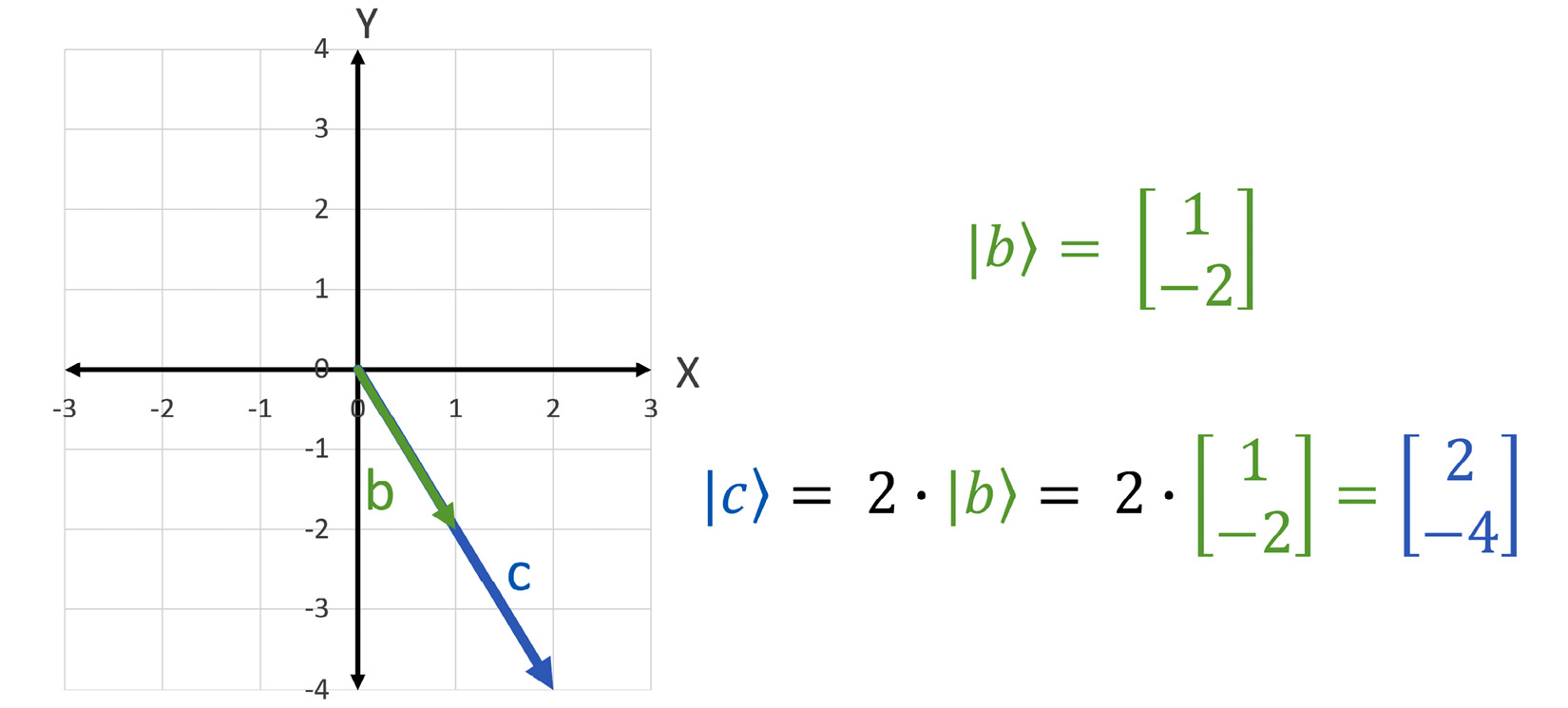
Figure 1.5 – Scalar multiplication

The vector |b⟩ is doubled or multiplied by two. Geometrically, we take the vector |b⟩ and scale its length by two while preserving its direction. Algebraically, we can just multiply the components of the vector by the number or scalar two.

Example

What is triple the vector |x⟩ shown here?

The solution is:

Exercise 2

• What is 4|x⟩?
• What is -2|x⟩?