The median of a dataset is the true middle value of the values sorted. Now, if there isn't a single middle value, such as if there's an even number of elements in the list, then we take the average of the two values closest to the sorted middle. In this video, we're going to discuss the algorithm for computing the median of a dataset, and we're going to take the traditional approach of sorting the values first and then selecting the values we need in order to compute the median. We're going to be testing the circumstances under which the median function should behave, and then we're going to compute the median of our 2015 away-team runs using our prototyped function.
In the last section, we were discussing the mean and standard deviation of runs; and we found that one standard deviation range was 1.03 to 7.27. Now, for this topic, we will have to add yet another import, and we're going to import Data.List, as this is where we find the sort function:
Now, as usual, we will restart and rerun all so that everything is properly loaded for our notebook. Next, let's create a couple of quick lists, just to demonstrate the sort function:
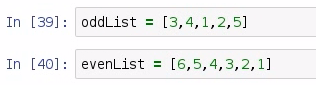
So, here we have oddList, which contains the comma-separated values "3,4,1,2,5", and we have an evenList, which contains "6,5,4,3,2,1". We can use the sort function to sort these lists as follows:

This was pretty straightforward—the sort function is found in the Data.List library. If we wish to find the middle value of a list, we need to find the length of the list and then divide by 2:
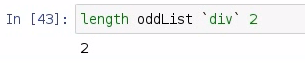
So, we have used the length of oddList and then divided it by 2, and it produces 2. Now we can sort that odd list and pull out the second element:
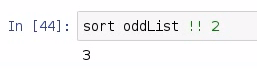
After sorting, we got 3; and 3 is the median of our odd list. And for an odd list, that's all you have to do.
Whenever we pass an even list, you should notice that we get the index position that appears after the median. So, if we divide the length of evenList by 2, we will get 3 as shown in the following screenshot:
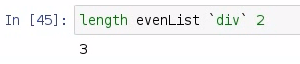
The index position for 3 in our sorted even list will be 4, which is not the median. So, we need to take the two values that are closest to the middle, which in this case it will be index 3; and then the index position before that, which is 2; and then add those together and divide by 2. So, the formula is as follows:

As we can see that our median is 3.5, which is the true median of our even list. There are algorithms for finding the median that do not require the full sort of values, such as you can use the quickselect algorithm to quickly find the median sorted value in a list. But for our purposes, we're going to stay with the traditional sort the values first approach. We're going to prototype a median function utilizing the approach that we've outlined here. We're going to go over a few quick examples of what should happen whenever median is called:
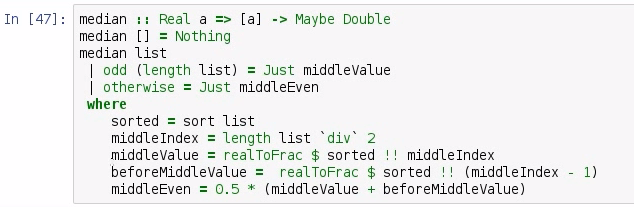
So, here is our median prototyped function. Notice that we are bounding our inputs based on type Real, and we are packaging once again a Double inside of a Maybe. We're using Double because, you know, there's the possibility that even though we have a full list of integers, we still need to return a double because we have an even number of integers. If we have a median of no items, then we return Nothing. Other than that, we are going to have the possibility of an odd list; then we will return the middleValue. Otherwise, we are going to return the middleEven. After that, we have outlined all of the different circumstances. So, let's test out a few examples:

Whenever we return the median of an empty list, we get Nothing. Likewise, if we get the median of oddList, we should get back 3. Notice it's been converted to a double. And if we do the median of an evenList, we get 3.5. And to outline again, we have our middleValue, which is just the middleIndex; and we have the beforeMiddleValue, which is middleIndex - 1. And the middleEven is simply those two values divided by 2; and that's all there really is to it. We're using the odd function in order to look for an odd number of elements; otherwise, we're going to use the even approach.
So, using sort, we built a function for finding the median of a list. This was a long function, and we described it in detail. Finally, we need to use the median function, which we have prototyped already, in order to find the away runs:
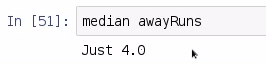
We found that the middle sorted value of array runs in the 2015 season is 4. In our next section, we are going to discuss what's probably the simplest of the descriptive statistics to discuss, and that is the mode, but it turns out to be one of the more difficult to compute.


























































