The independence of probabilistic events
We say that the two events E and F are independent if P(F|E) = P(F). In other words, the occurrence of E has no effect upon the probability of F. From the previous formula, we can see that this definition is equivalent to the condition:
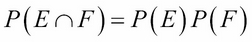
This shows that the definition is symmetric: E is independent of F if and only if F is independent of E.
In our preceding marble example, E = (1st is R) and let F = (2nd is G). Since P(F|E) = 80% and P(F) = 67%, we see that E and F are not independent. Obviously, F depends on E.
For another example, consider the previous Motor Vehicle example. Let E = (driver owns 2 vehicles) and F = (driver drives at least 10,000 miles/year). We can compute the unconditional probabilities from the marginal data: P(E) = 0.31 and P(F) = 0.36 + 0.19 = 0.55. So P(E)P(F) = (0.31)(0.55) = 0.17. But P(E ∩ F)= 0.12 + 0.08 = 0.20 ≠ 0.17, so these two events are not independent. Whether a person drives a lot depends upon the number of vehicles...



























































