Vectorizing text

While building models for the SMS message spam detection thus far, only aggregate features based on counts or distributions of lexical or grammatical features have been considered. The actual words in the messages have not been used thus far. There are a couple of challenges in using the text content of messages. The first is that text can be of arbitrary lengths. Comparing this to image data, we know that each image has a fixed width and height. Even if the corpus of images has a mixture of sizes, images can be resized to a common size with minimal loss of information by using a variety of compression mechanisms. In NLP, this is a bigger problem compared to computer vision. A common approach to handle this is to truncate the text. We will see various ways to handle variable-length texts in various examples throughout the book.

The second issue is that of the representation of words with a numerical quantity or feature. In computer vision, the smallest unit is a pixel. Each pixel has a set of numerical values indicating color or intensity. In a text, the smallest unit could be a word. Aggregating the Unicode values of the characters does not convey or embody the meaning of the word. In fact, these character codes embody no information at all about the character, such as its prevalence, whether it is a consonant or a vowel, and so on. However, averaging the pixels in a section of an image could be a reasonable approximation of that region of the image. It may represent how that region would look if seen from a large distance. A core problem then is to construct a numerical representation of words. Vectorization is the process of converting a word to a vector of numbers that embodies the information contained in the word. Depending on the vectorization technique, this vector may have additional properties that may allow comparison with other words, as will be shown in the Word vectors section later in this chapter.

The simplest approach for vectorizing is to use counts of words. The second approach is more sophisticated, with its origins in information retrieval, and is called TF-IDF. The third approach is relatively new, having been published in 2013, and uses RNNs to generate embeddings or word vectors. This method is called Word2Vec. The newest method in this area as of the time of writing was BERT, which came out in the last quarter of 2018. The first three methods will be discussed in this chapter. BERT will be discussed in detail in Chapter 3, Named Entity Recognition (NER) with BiLSTMs, CRFs, and Viterbi Decoding.

Count-based vectorization

The idea behind count-based vectorization is really simple. Each unique word appearing in the corpus is assigned a column in the vocabulary. Each document, which would correspond to individual messages in the spam example, is assigned a row. The counts of the words appearing in that document are entered in the relevant cell corresponding to the document and the word. With n unique documents containing m unique words, this results in a matrix of n rows by m columns. Consider a corpus like so:

corpus = [
          "I like fruits. Fruits like bananas",
          "I love bananas but eat an apple",
          "An apple a day keeps the doctor away"
]

There are three documents in this corpus of text. The scikit-learn (sklearn) library provides methods for undertaking count-based vectorization.

Modeling after count-based vectorization

In Google Colab, this library should already be installed. If it is not installed in your Python environment, it can be installed via the notebook like so:

!pip install sklearn

The CountVectorizer class provides a built-in tokenizer that separates the tokens of two or more characters in length. This class takes a variety of options including a custom tokenizer, a stop word list, the option to convert characters to lowercase prior to tokenization, and a binary mode that converts every positive count to 1. The defaults provide a reasonable choice for an English language corpus:

from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(corpus)
vectorizer.get_feature_names()

['an',
 'apple',
 'away',
 'bananas',
 'but',
 'day',
 'doctor',
 'eat',
 'fruits',
 'keeps',
 'like',
 'love',
 'the']

In the preceding code, a model is fit to the corpus. The last line prints out the tokens that are used as columns. The full matrix can be seen as follows:

X.toarray()

array([[0, 0, 0, 1, 0, 0, 0, 0, 2, 0, 2, 0, 0],
       [1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0],
       [1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1]])

This process has now converted a sentence such as "I like fruits. Fruits like bananas" into a vector (0, 0, 0, 1, 0, 0, 0, 2, 0, 2, 0, 0). This is an example of context-free vectorization. Context-free refers to the fact that the order of the words in the document did not make any difference in the generation of the vector. This is merely counting the instances of the words in a document. Consequently, words with multiple meanings may be grouped into one, for example, bank. This may refer to a place near the river or a place to keep money. However, it does provide a method to compare documents and derive similarity. The cosine similarity or distance can be computed between two documents, to see which documents are similar to which other documents:

from sklearn.metrics.pairwise import cosine_similarity
cosine_similarity(X.toarray())
array([[1.        , 0.13608276, 0.        ],
       [0.13608276, 1.        , 0.3086067 ],
       [0.        , 0.3086067 , 1.        ]])

This shows that the first sentence and the second sentence have a 0.136 similarity score (on a scale of 0 to 1). The first and third sentence have nothing in common. The second and third sentence have a similarity score of 0.308 – the highest in this set. Another use case of this technique is to check the similarity of the documents with given keywords. Let's say that the query is apple and bananas. This first step is to compute the vector of this query, and then compute the cosine similarity scores against the documents in the corpus:

query = vectorizer.transform(["apple and bananas"])
cosine_similarity(X, query)
array([[0.23570226],
       [0.57735027],
       [0.26726124]])

This shows that this query matches the second sentence in the corpus the best. The third sentence would rank second, and the first sentence would rank lowest. In a few lines, a basic search engine has been implemented, along with logic to serve queries! At scale, this is a very difficult problem, as the number of words or columns in a web crawler would top 3 billion. Every web page would be represented as a row, so that would also require billions of rows. Computing a cosine similarity in milliseconds to serve an online query and keeping the content of this matrix updated is a massive undertaking.

The next step from this rather simple vectorization scheme is to consider the information content of each word in constructing this matrix.

Term Frequency-Inverse Document Frequency (TF-IDF)

In creating a vector representation of the document, only the presence of words was included – it does not factor in the importance of a word. If the corpus of documents being processed is about a set of recipes with fruits, then one may expect words like apples, raspberries, and washing to appear frequently. Term Frequency (TF) represents how often a word or token occurs in a given document. This is exactly what we did in the previous section. In a set of documents about fruits and cooking, a word like apple may not be terribly specific to help identify a recipe. However, a word like tuile may be uncommon in that context. Therefore, it may help to narrow the search for recipes much faster than a word like raspberry. On a side note, feel free to search the web for raspberry tuile recipes. If a word is rare, we want to give it a higher weight, as it may contain more information than a common word. A term can be upweighted by the inverse of the number of documents it appears in. Consequently, words that occur in a lot of documents will get a smaller score compared to terms that appear in fewer documents. This is called the Inverse Document Frequency (IDF).

Mathematically, the score of each term in a document can be computed as follows:

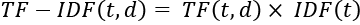
Here, t represents the word or term, and d represents a specific document.

It is common to normalize the TF of a term in a document by the total number of tokens in that document.

The IDF is defined as follows:

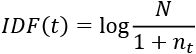
Here, N represents the total number of documents in the corpus, and n_t represents the number of documents where the term is present. The addition of 1 in the denominator avoids the divide-by-zero error. Fortunately, sklearn provides methods to compute TF-IDF.

The TF-IDF Vectorization section of the notebook contains the code for this section.

Let's convert the counts from the previous section into their TF-IDF equivalents:

import pandas as pd
from sklearn.feature_extraction.text import TfidfTransformer
transformer = TfidfTransformer(smooth_idf=False)
tfidf = transformer.fit_transform(X.toarray())
pd.DataFrame(tfidf.toarray(), 
             columns=vectorizer.get_feature_names())

This produces the following output:

This should give some intuition on how TF-IDF is computed. Even with three toy sentences and a very limited vocabulary, many of the columns in each row are 0. This vectorization produces sparse representations.

Now, this can be applied to the problem of detecting spam messages. Thus far, the features for each message have been computed based on some aggregate statistics and added to the pandas DataFrame. Now, the content of the message will be tokenized and converted into a set of columns. The TF-IDF score for each word or token will be computed for each message in the array. This is surprisingly easy to do with sklearn, as follows:

from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn. pre-processing import LabelEncoder
tfidf = TfidfVectorizer(binary=True)
X = tfidf.fit_transform(train['Message']).astype('float32')
X_test = tfidf.transform(test['Message']).astype('float32')
X.shape

(4459, 7741)

The second parameter shows that 7,741 tokens were uniquely identified. These are the columns of features that will be used in the model later. Note that the vectorizer was created with the binary flag. This implies that even if a token appears multiple times in a message, it is counted as one. The next line trains the TF-IDF model on the training dataset. Then, it converts the words in the test set according to the TF-IDF scores learned from the training set. Let's train a model on just these TF-IDF features.

Modeling using TF-IDF features

With these TF-IDF features, let's train a model and see how it does:

_, cols = X.shape
model2 = make_model(cols)  # to match tf-idf dimensions
y_train = train[['Spam']]
y_test = test[['Spam']]
model2.fit(X.toarray(), y_train, epochs=10, batch_size=10)

Train on 4459 samples
Epoch 1/10
4459/4459 [==============================] - 2s 380us/sample - loss: 0.3505 - accuracy: 0.8903
...
Epoch 10/10
4459/4459 [==============================] - 1s 323us/sample - loss: 0.0027 - accuracy: 1.0000

Whoa – we are able to classify every one correctly! In all honesty, the model is probably overfitting, so some regularization should be applied. The test set gives this result:

model2.evaluate(X_test.toarray(), y_test)

1115/1115 [==============================] - 0s 134us/sample - loss: 0.0581 - accuracy: 0.9839
[0.05813191874545786, 0.9838565]

An accuracy rate of 98.39% is by far the best we have gotten in any model so far. Checking the confusion matrix, it is evident that this model is indeed doing very well:

y_test_pred = model2.predict_classes(X_test.toarray())
tf.math.confusion_matrix(tf.constant(y_test.Spam), 
                         y_test_pred)
<tf.Tensor: shape=(2, 2), dtype=int32, numpy=
array([[958,   2],
       [ 16, 139]], dtype=int32)>

Only 2 regular messages were classified as spam, while only 16 spam messages were classified as being not spam. This is indeed a very good model. Note that this dataset has Indonesian (or Bahasa) words as well as English words in it. Bahasa uses the Latin alphabet. This model, without using a lot of pretraining and knowledge of language, vocabulary, and grammar, was able to do a very reasonable job with the task at hand.

However, this model ignores the relationships between words completely. It treats the words in a document as unordered items in a set. There are better models that vectorize the tokens in a way that preserves some of the relationships between the tokens. This is explored in the next section.

Word vectors

In the previous example, a row vector was used to represent a document. This was used as a feature for the classification model to predict spam labels. However, no information can be gleaned reliably from the relationships between words. In NLP, a lot of research has been focused on learning the words or representations in an unsupervised way. This is called representation learning. The output of this approach is a representation of a word in some vector space, and the word can be considered embedded in that space. Consequently, these word vectors are also called embeddings.

The core hypothesis behind word vector algorithms is that words that occur near each other are related to each other. To see the intuition behind this, consider two words, bake and oven. Given a sentence fragment of five words, where one of these words is present, what would be the probability of the other being present as well? You would be right in guessing that the probability is likely quite high. Suppose now that words are being mapped into some two-dimensional space. In that space, these two words should be closer to each other, and probably further away from words like astronomy and tractor.

The task of learning these embeddings for the words can be then thought of as adjusting words in a giant multidimensional space where similar words are closer to each other and dissimilar words are further apart from each other.

A revolutionary approach to do this is called Word2Vec. This algorithm was published by Tomas Mikolov and collaborators from Google in 2013. This approach produces dense vectors of the order of 50-300 dimensions generally (though larger are known), where most of the values are non-zero. In contrast, in our previous trivial spam example, the TF-IDF model had 7,741 dimensions. The original paper had two algorithms proposed in it: continuous bag-of-words and continuous skip-gram. On semantic tasks and overall, the performance of skip-gram was state of the art at the time of its publication. Consequently, the continuous skip-gram model with negative sampling has become synonymous with Word2Vec. The intuition behind this model is fairly straightforward.

Consider this sentence fragment from a recipe: "Bake until the cookie is golden brown all over." Under the assumption that a word is related to the words that appear near it, a word from this fragment can be picked and a classifier can be trained to predict the words around it:

Figure 1.14: A window of 5 centered on cookie

Taking an example of a window of five words, the word in the center is used to predict two words before and two words after it. In the preceding figure, the fragment is until the cookie is golden, with the focus on the word cookie. Assuming that there are 10,000 words in the vocabulary, a network can be trained to predict binary decisions given a pair of words. The training objective is that the network predicts true for pairs like (cookie, golden) while predicting false for (cookie, kangaroo). This particular approach is called Skip-Gram Negative Sampling (SGNS) and it considerably reduces the training time required for large vocabularies. Very similar to the single-layer neural model in the previous section, a model can be trained with a one-to-many as the output layer. The sigmoid activation would be changed to a softmax function. If the hidden layer has 300 units, then its dimensions would be 10,000 x 300, that is, for each of the words, there will be a set of weights. The objective of the training is to learn these weights. In fact, these weights become the embedding for that word once training is complete.

The choice of units in the hidden layer is a hyperparameter that can be adapted for specific applications. 300 is commonly found as it is available through pretrained embeddings on the Google News dataset. Finally, the error is computed as the sum of the categorical cross-entropy of all the word pairs in negative and positive examples.

The beauty of this model is that it does not require any supervised training data. Running sentences can be used to provide positive examples. For the model to learn effectively, it is important to provide negative samples as well. Words are randomly sampled using their probability of occurrence in the training corpus and fed as negative examples.

To understand how the Word2Vec embeddings work, let's download a set of pretrained embeddings.

The code shown in the following section can be found in the Word Vectors section of the notebook.

Pretrained models using Word2Vec embeddings

Since we are only interested in experimenting with a pretrained model, we can use the Gensim library and its pretrained embeddings. Gensim should already be installed in Google Colab. It can be installed like so:

!pip install gensim

After the requisite imports, pretrained embeddings can be downloaded and loaded. Note that these particular embeddings are approximately 1.6 GB in size, so may take a very long time to load (you may encounter some memory issues as well):

from gensim.models.word2vec import Word2Vec
import gensim.downloader as api
model_w2v = api.load("word2vec-google-news-300")

Another issue that you may run into is the Colab session expiring if left alone for too long while waiting for the download to finish. This may be a good time to switch to a local notebook, which will also be helpful in future chapters. Now, we are ready to inspect the similar words:

model_w2v.most_similar("cookies",topn=10)

[('cookie', 0.745154082775116),
 ('oatmeal_raisin_cookies', 0.6887780427932739),
 ('oatmeal_cookies', 0.662139892578125),
 ('cookie_dough_ice_cream', 0.6520504951477051),
 ('brownies', 0.6479344964027405),
 ('homemade_cookies', 0.6476464867591858),
 ('gingerbread_cookies', 0.6461867690086365),
 ('Cookies', 0.6341644525527954),
 ('cookies_cupcakes', 0.6275068521499634),
 ('cupcakes', 0.6258294582366943)]

This is pretty good. Let's see how this model does at a word analogy task:

model_w2v.doesnt_match(["USA","Canada","India","Tokyo"])

'Tokyo'

The model is able to guess that compared to the other words, which are all countries, Tokyo is the odd one out, as it is a city. Now, let's try a very famous example of mathematics on these word vectors:

king = model_w2v['king']
man = model_w2v['man']
woman = model_w2v['woman']
queen = king - man + woman  
model_w2v.similar_by_vector(queen)

[('king', 0.8449392318725586),
 ('queen', 0.7300517559051514),
 ('monarch', 0.6454660892486572),
 ('princess', 0.6156251430511475),
 ('crown_prince', 0.5818676948547363),
 ('prince', 0.5777117609977722),
 ('kings', 0.5613663792610168),
 ('sultan', 0.5376776456832886),
 ('Queen_Consort', 0.5344247817993164),
 ('queens', 0.5289887189865112)]

Given that King was provided as an input to the equation, it is simple to filter the inputs from the outputs and Queen would be the top result. SMS spam classification could be attempted using these embeddings. However, future chapters will cover the use of GloVe embeddings and BERT embeddings for sentiment analysis.

A pretrained model like the preceding can be used to vectorize a document. Using these embeddings, models can be trained for specific purposes. In later chapters, newer methods of generating contextual embeddings, such as BERT, will be discussed in detail.