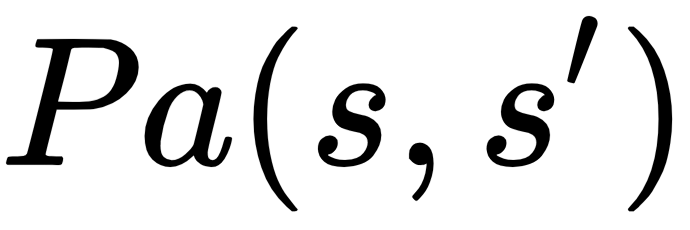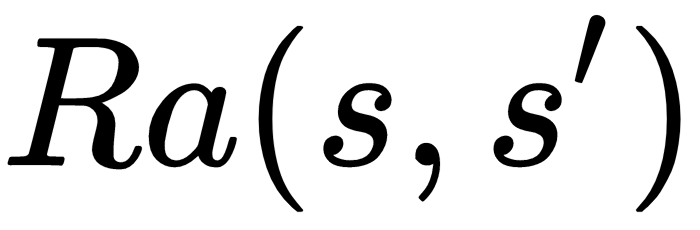How to be an adaptive thinker

Reinforcement learning, one of the foundations of machine learning, supposes learning through trial and error by interacting with an environment. This sounds familiar, right? That is what we humans do all our lives—in pain! Try things, evaluate, and then continue; or try something else.

In real life, you are the agent of your thought process. In a machine learning model, the agent is the function calculating through this trial-and-error process. This thought process in machine learning is the MDP. This form of action-value learning is sometimes called Q.

To master the outcomes of MDP in theory and practice, a three-dimensional method is a prerequisite.

The three-dimensional approach that will make you an artificial expert, in general terms, means:

• Starting by describing a problem to solve with real-life cases
• Then, building a mathematical model
• Then, write source code and/or using a cloud platform solution

It is a way for you to enter any project with an adaptive attitude from the outset.

Addressing real-life issues before coding a solution

In this chapter, we are going to tackle Markov's Decision Process (Q function) and apply it to reinforcement learning with the Bellman equation. You can find tons of source code and examples on the web. However, most of them are toy experiments that have nothing to do with real life. For example, reinforcement learning can be applied to an e-commerce business delivery person, self-driving vehicle, or a drone. You will find a program that calculates a drone delivery. However, it has many limits that need to be overcome. You as an adaptive thinker are going to ask some questions:

• What if there are 5,000 drones over a major city at the same time?
• Is a drone-jam legal? What about the noise over the city? What about tourism?
• What about the weather? Weather forecasts are difficult to make, so how is this scheduled?

In just a few minutes, you will be at the center of attention, among theoreticians who know more than you on one side and angry managers who want solutions they cannot get on the other side. Your real-life approach will solve these problems.

A foolproof method is the practical three-dimensional approach:

• Be a subject matter expert (SME): First, you have to be an SME. If a theoretician geek comes up with a hundred Google DeepMind TensorFlow functions to solve a drone trajectory problem, you now know it is going to be a tough ride if real-life parameters are taken into account.
  An SME knows the subject and thus can quickly identify the critical factors of a given field. Artificial intelligence often requires finding a solution to a hard problem that even an expert in a given field cannot express mathematically. Machine learning sometimes means finding a solution to a problem that humans do not know how to explain. Deep learning, involving complex networks, solves even more difficult problems.
• Have enough mathematical knowledge to understand AI concepts: Once you have the proper natural language analysis, you need to build your abstract representation quickly. The best way is to look around at your everyday life and make a mathematical model of it. Mathematics is not an option in AI, but a prerequisite. The effort is worthwhile. Then, you can start writing solid source code or start implementing a cloud platform ML solution.
• Know what source code is about as well as its potential and limits: MDP is an excellent way to go and start working in the three dimensions that will make you adaptive: describing what is around you in detail in words, translating that into mathematical representations, and then implementing the result in your source code.

Step 1 – MDP in natural language

Step 1 of any artificial intelligence problem is to transpose it into something you know in your everyday life (work or personal). Something you are an SME in. If you have a driver's license, then you are an SME of driving. You are certified. If you do not have a driver's license or never drive, you can easily replace moving around in a car by moving around on foot.

Let's say you are an e-commerce business driver delivering a package in an area you do not know. You are the operator of a self-driving vehicle. You have a GPS system with a beautiful color map on it. The areas around you are represented by the letters A to F, as shown in the simplified map in the following diagram. You are presently at F. Your goal is to reach area C. You are happy, listening to the radio. Everything is going smoothly, and it looks like you are going to be there on time. The following graph represents the locations and routes that you can possibly cover.

The guiding system's state indicates the complete path to reach C. It is telling you that you are going to go from F to B to D and then to C. It looks good!

To break things down further, let's say:

• The present state is the letter s.
• Your next action is the letter a (action). This action a is not location A.
• The next action a (not location A) is to go to location B. You look at your guiding system; it tells you there is no traffic, and that to go from your present state F to your next state B will take you only a few minutes. Let's say that the next state B is the letter B.

At this point, you are still quite happy, and we can sum up your situation with the following sequence of events:

The letter s is your present state, your present situation. The letter a is the action you're deciding, which is to go to the next area; there you will be in another state, s'. We can say that thanks to the action a, you will go from s to s'.

Now, imagine that the driver is not you anymore. You are tired for some reason. That is when a self-driving vehicle comes in handy. You set your car to autopilot. Now you are not driving anymore; the system is. Let's call that system the agent. At point F, you set your car to autopilot and let the self-driving agent take over.

The agent now sees what you have asked it to do and checks its mapping environment, which represents all the areas in the previous diagram from A to F.

In the meantime, you are rightly worried. Is the agent going to make it or not? You are wondering if its strategy meets yours. You have your policy P—your way of thinking—which is to take the shortest paths possible. Will the agent agree? What's going on in its mind? You observe and begin to realize things you never noticed before. Since this is the first time you are using this car and guiding system, the agent is memoryless, which is an MDP feature. This means the agent just doesn't know anything about what went on before. It seems to be happy with just calculating from this state s at area F. It will use machine power to run as many calculations as necessary to reach its goal.

Another thing you are watching is the total distance from F to C to check whether things are OK. That means that the agent is calculating all the states from F to C.

In this case, state F is state 1, which we can simplify by writing s₁. B is state 2, which we can simplify by write s₂. D is s₃ and C is s₄. The agent is calculating all of these possible states to make a decision.

The agent knows that when it reaches D, C will be better because the reward will be higher to go to C than anywhere else. Since it cannot eat a piece of cake to reward itself, the agent uses numbers. Our agent is a real number cruncher. When it is wrong, it gets a poor reward or nothing in this model. When it's right, it gets a reward represented by the letter R. This action-value (reward) transition, often named the Q function, is the core of many reinforcement learning algorithms.

When our agent goes from one state to another, it performs a transition and gets a reward. For example, the transition can be from F to B, state 1 to state 2, or s₁ to s_2.

You are feeling great and are going to be on time. You are beginning to understand how the machine learning agent in your self-driving car is thinking. Suddenly your guiding system breaks down. All you can see on the screen is that static image of the areas of the last calculation. You look up and see that a traffic jam is building up. Area D is still far away, and now you do not know whether it would be good to go from D to C or D to E to get a taxi that can take special lanes. You are going to need your agent!

The agent takes the traffic jam into account, is stubborn, and increases its reward to get to C by the shortest way. Its policy is to stick to the initial plan. You do not agree. You have another policy.

You stop the car. You both have to agree before continuing. You have your opinion and policy; the agent does not agree. Before continuing, your views need to converge. Convergence is the key to making sure that your calculations are correct. This is the kind of problem that persons, or soon, self-driving vehicles (not to speak about drone air jams), delivering parcels encounter all day long to get the workload done. The number of parcels to delivery per hour is an example of the workload that needs to be taken into account when making a decision.

To represent the problem at this point, the best way is to express this whole process mathematically.

Step 2 – the mathematical representation of the Bellman equation and MDP

Mathematics involves a whole change in your perspective of a problem. You are going from words to functions, the pillars of source coding.

Expressing problems in mathematical notation does not mean getting lost in academic math to the point of never writing a single line of code. Mathematics is viewed in the perspective of getting a job done. Skipping mathematical representation will fast-track a few functions in the early stages of an AI project. However, when the real problems that occur in all AI projects surface, solving them with source code only will prove virtually impossible. The goal here is to pick up enough mathematics to implement a solution in real-life companies.

It is necessary to think of a problem through by finding something familiar around us, such as the delivery itinerary example covered before. It is a good thing to write it down with some abstract letters and symbols as described before, with a meaning an action and s meaning a state. Once you have understood the problem and expressed the parameters in a way you are used to, you can proceed further.

Now, mathematics well help clarify the situation by shorter descriptions. With the main ideas in mind, it is time to convert them into equations.

From MDP to the Bellman equation

In the previous step 1, the agent went from F or state 1 or s to B, which was state 2 or s'.

To do that, there was a strategy—a policy represented by P. All of this can be shown in one mathematical expression, the MDP state transition function:

P is the policy, the strategy made by the agent to go from F to B through action a. When going from F to B, this state transition is called state transition function:

• a is the action
• s is state 1 (F) and s' is state 2 (B)

This is the basis of MDP. The reward (right or wrong) is represented in the same way:

That means R is the reward for the action of going from state s to state s'. Going from one state to another will be a random process. This means that potentially, all states can go to another state.

The example we will be working on inputs a reward matrix so that the program can choose its best course of action. Then, the agent will go from state to state, learning the best trajectories for every possible starting location point. The goal of the MDP is to go to C (line 3, column 3 in the reward matrix), which has a starting value of 100 in the following Python code.

# Markov Decision Process (MDP) - The Bellman equations adapted to
# Reinforcement Learning
# R is The Reward Matrix for each state
R = ql.matrix([ [0,0,0,0,1,0],
                [0,0,0,1,0,1],
                [0,0,100,1,0,0],
                [0,1,1,0,1,0],
                [1,0,0,1,0,0],
                [0,1,0,0,0,0] ])

Each line in the matrix in the example represents a letter from A to F, and each column represents a letter from A to F. All possible states are represented. The 1 values represent the nodes (vertices) of the graph. Those are the possible locations. For example, line 1 represents the possible moves for letter A, line 2 for letter B, and line 6 for letter F. On the first line, A cannot go to C directly, so a 0 value is entered. But, it can go to E, so a 1 value is added.

Some models start with -1 for impossible choices, such as B going directly to C and 0 values to define the locations. This model starts with 0 and 1 values. It sometimes takes weeks to design functions that will create a reward matrix (see Chapter 2, Think like a Machine).

There are several properties of this decision process. A few of them are mentioned here:

• The Markov property: The process is applied when the past is not taken into account. It is the memoryless property of this decision process, just as you do in a car with a guiding system. You move forward to reach your goal. This is called the Markov property.
• Unsupervised learning: From this memoryless Markov property, it is safe to say that the MDP is not supervised learning. Supervised learning would mean that we would have all the labels of the trip. We would know exactly what A means and use that property to make a decision. We would be in the future looking at the past. MDP does not take these labels into account. This means that this is unsupervised learning. A decision has to be made in each state without knowing the past states or what they signify. It means that the car, for example, was on its own at each location, which is represented by each of its states.
• Stochastic process: In step 1, when state B was reached, the agent controlling the mapping system and the driver didn't agree on where to go. A random choice could be made in a trial-and-error way, just like a coin toss. It is going to be a heads-or-tails process. The agent will toss the coin thousands of times and measure the outcomes. That's precisely how MDP works and how the agent will learn.
• Reinforcement learning: Repeating a trial and error process with feedback from the agent's environment.
• Markov chain: The process of going from state to state with no history in a random, stochastic way is called a Markov chain.

To sum it up, we have three tools:

• P_a(s,s'): A policy, P, or strategy to move from one state to another
• T_a(s,s'): A T, or stochastic (random) transition, function to carry out that action
• R_a(s,s'): An R, or reward, for that action, which can be negative, null, or positive

T is the transition function, which makes the agent decide to go from one point to another with a policy. In this case, it will be random. That's what machine power is for, and that's how reinforcement learning is often implemented.

Randomness is a property of MDP.

The following code describes the choice the agent is going to make.

next_action = int(ql.random.choice(PossibleAction,1))
return next_action

Once the code has been run, a new random action (state) has been chosen.

The Bellman equation is the road to programming reinforcement learning.

Bellman's equation completes the MDP. To calculate the value of a state, let's use Q, for the Q action-reward (or value) function. The pre-source code of Bellman's equation can be expressed as follows for one individual state:

The source code then translates the equation into a machine representation as in the following code:

# The Bellman equation
    Q[current_state, action] = R[current_state, action] + gamma * MaxValue

The source code variables of the Bellman equation are as follows:

• Q(s): This is the value calculated for this state—the total reward. In step 1 when the agent went from F to B, the driver had to be happy. Maybe she/he had a crunch in a candy bar to feel good, which is the human counterpart of the reward matrix. The automatic driver maybe ate (reward matrix) some electricity, renewable energy of course! The reward is a number such as 50 or 100 to show the agent that it's on the right track. It's like when a student gets a good grade in an exam.
• R(s): This is the sum of the values up to there. It's the total reward at that point.
• ϒ = gamma: This is here to remind us that trial and error has a price. We're wasting time, money, and energy. Furthermore, we don't even know whether the next step is right or wrong since we're in a trial-and-error mode. Gamma is often set to 0.8. What does that mean? Suppose you're taking an exam. You study and study, but you don't really know the outcome. You might have 80 out of 100 (0.8) chances of clearing it. That's painful, but that's life. This is what makes Bellman's equation and MDP realistic and efficient.
• max(s'): s' is one of the possible states that can be reached with P_a (s,s'); max is the highest value on the line of that state (location line in the reward matrix).

Step 3 – implementing the solution in Python

In step 1, a problem was described in natural language to be able to talk to experts and understand what was expected. In step 2, an essential mathematical bridge was built between natural language and source coding. Step 3 is the software implementation phase.

When a problem comes up—and rest assured that one always does—it will be possible to go back over the mathematical bridge with the customer or company team, and even further back to the natural language process if necessary.

This method guarantees success for any project. The code in this chapter is in Python 3.6. It is a reinforcement learning program using the Q function with the following reward matrix:

import numpy as ql
R = ql.matrix([ [0,0,0,0,1,0],
                [0,0,0,1,0,1],
                [0,0,100,1,0,0],
                [0,1,1,0,1,0],
                [1,0,0,1,0,0],
                [0,1,0,0,0,0] ])

Q = ql.matrix(ql.zeros([6,6]))

gamma = 0.8

R is the reward matrix described in the mathematical analysis.

Q inherits the same structure as R, but all values are set to 0 since this is a learning matrix. It will progressively contain the results of the decision process. The gamma variable is a double reminder that the system is learning and that its decisions have only an 80% chance of being correct each time. As the following code shows, the system explores the possible actions during the process.

agent_s_state = 1

# The possible "a" actions when the agent is in a given state
def possible_actions(state):
      current_state_row = R[state,]
      possible_act = ql.where(current_state_row >0)[1]
      return possible_act

# Get available actions in the current state
PossibleAction = possible_actions(agent_s_state) 

The agent starts in state 1, for example. You can start wherever you want because it's a random process. Note that only values > 0 are taken into account. They represent the possible moves (decisions).

The current state goes through an analysis process to find possible actions (next possible states). You will note that there is no algorithm in the traditional sense with many rules. It's a pure random calculation, as the following random.choice function shows.

def ActionChoice(available_actions_range):
    next_action = int(ql.random.choice(PossibleAction,1))
    return next_action

# Sample next action to be performed
action = ActionChoice(PossibleAction)

Now comes the core of the system containing Bellman's equation, translated into the following source code:

def reward(current_state, action, gamma):
    Max_State = ql.where(Q[action,] == ql.max(Q[action,]))[1]

    if Max_State.shape[0] > 1:
        Max_State = int(ql.random.choice(Max_State, size = 1))
    else:
        Max_State = int(Max_State)
    MaxValue = Q[action, Max_State]
    
    # Q function
    Q[current_state, action] = R[current_state, action] + gamma * MaxValue

# Rewarding Q matrix
reward(agent_s_state,action,gamma)

You can see that the agent looks for the maximum value of the next possible state chosen at random.

The best way to understand this is to run the program in your Python environment and print() the intermediate values. I suggest that you open a spreadsheet and note the values. It will give you a clear view of the process.

The last part is simply about running the learning process 50,000 times, just to be sure that the system learns everything there is to find. During each iteration, the agent will detect its present state, choose a course of action, and update the Q function matrix:

for i in range(50000):
    current_state = ql.random.randint(0, int(Q.shape[0]))
    PossibleAction = possible_actions(current_state)
    action = ActionChoice(PossibleAction)
    reward(current_state,action,gamma)
    
# Displaying Q before the norm of Q phase
print("Q :")
print(Q)

# Norm of Q
print("Normed Q :")
print(Q/ql.max(Q)*100)

After the process is repeated and until the learning process is over, the program will print the result in Q and the normed result. The normed result is the process of dividing all values by the sum of the values found. The result comes out as a normed percentage.

View the Python program at https://github.com/PacktPublishing/Artificial-Intelligence-By-Example/blob/master/Chapter01/MDP.py.