Univariate time series analysis

We will focus on two methods to analyze and forecast a single time series: exponential smoothing and Autoregressive Integrated Moving Average (ARIMA) models. We will start by looking at exponential smoothing models.

Exponential smoothing models use weights for past observations, such as a moving average model, but unlike moving average models, the more recent the observation, the more weight it is given, relative to the later ones. There are three possible smoothing parameters to estimate: the overall smoothing parameter, a trend parameter, and smoothing parameter. If no trend or seasonality is present, then these parameters become null.

The smoothing parameter produces a forecast with the following equation:

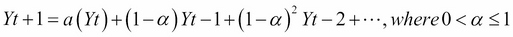
In this equation, Yt is the value at the time, T, and alpha (α) is the smoothing parameter. Algorithms optimize the alpha (and other parameters) by minimizing the errors, for example, sum of squared error (SSE) or mean squared error (MSE).

The forecast equation...