20.4 Padding oracle attacks on TLS handshake
The term oracle originally comes from complexity theory, where it is used to compare the complexity of two computational problems P1,P2.
Suppose we can solve P1 efficiently (i.e., in polynomial time), if there is a polynomial-time algorithm A to solve P2. In this situation, we say that P1 polytime reduces to P2, or
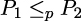
Informally, we can say that P2 is at least as hard as P1 ([117]). Now, the (hypothetical) algorithm A that can efficiently solve P2 is called an oracle for P2.
As an example, let P1 be the RSA-problem and P2 be the integer factorization problem. Recall from Chapter 7, Public-Key Cryptography, that the RSA problem means we have to find the plaintext m, given the ciphertext

and the public key (e,n), while the integer factorization problems is to find the prime factors of a given integer.
Now it is easy to see that if we had an oracle that provides us with the prime factors of n in polynomial time, we could also solve the...
























































