This section mainly focuses on how images are represented on a computer and how to feed this to the neural network. Based on what we've learned so far, neural networks predict only binary classes, where the answer is yes or no, or right or wrong. Consider the example of predicting whether a patient would have heart disease or not. The answer to this is binary in nature—yes or no. We will now learn to train our neural network to predict multiple classes using softmax.
A computer perceives an image as a two-dimensional matrix of numbers. Look at the following diagram:
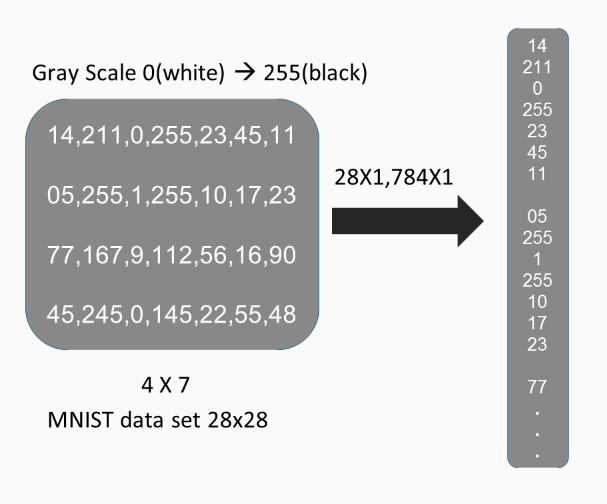
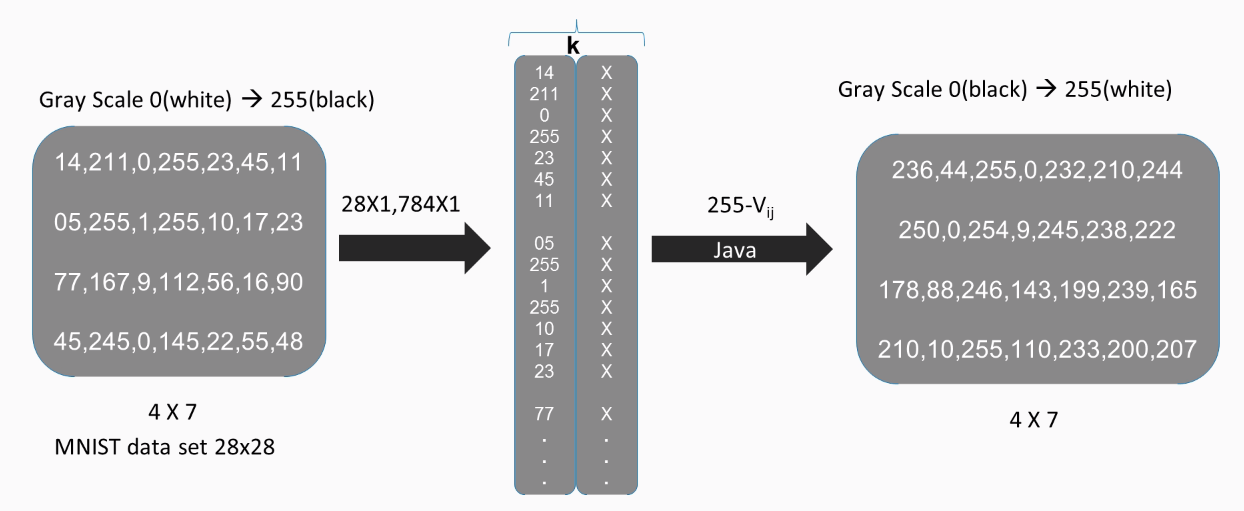
These numbers make little sense to us, but to a computer they mean everything. For a black-and-white image, each of these pixel values depicts the intensity of the light, so zero means white, and as we move closer to the number 255, the pixel gets darker. In this case, we considered an image with the dimensions 4 x 7. Images of the MNIST database are actually 28 x 28 in size. In order to make an image ready for processing, we need to transform it to a one-dimensional vector, which means that a 28 x 28 image will be transformed to 784 x 1 image and a 4 x 7 image to a 28 x 1.
Notice now how this one-dimensional vector is no different from a binary class case. Each of these pixels now is just a feature for a computer vision application. We can, of course, add k-images representations, if we choose a mini-batch gradient descent, which would process k-images in parallel.
When using Java, the values are parameters and their significance is inverse in nature. Here, 0 means black and 255 means white. In order to correctly depict an MNIST dataset image using Java, we need to use the  formula, where
formula, where  is the value of the pixel. This happens to be the case with most languages similar to Java:
is the value of the pixel. This happens to be the case with most languages similar to Java:
For colored images, consider an RGB-color JPG, which has a size of 260 x 194 pixels. The computer will see it as a three-dimensional matrix of numbers. Specifically, it will see it as 260 x 194 x 3. Each of the dimensions represents the intensity of the red color, the green color, and the blue color:
So if we take the red example, 0 means the color black, and 255 will be completely red. The same logic applies to the green and the blue colors. We need to transform the three-dimensional matrix to a one-dimensional vector, just as we did previously:
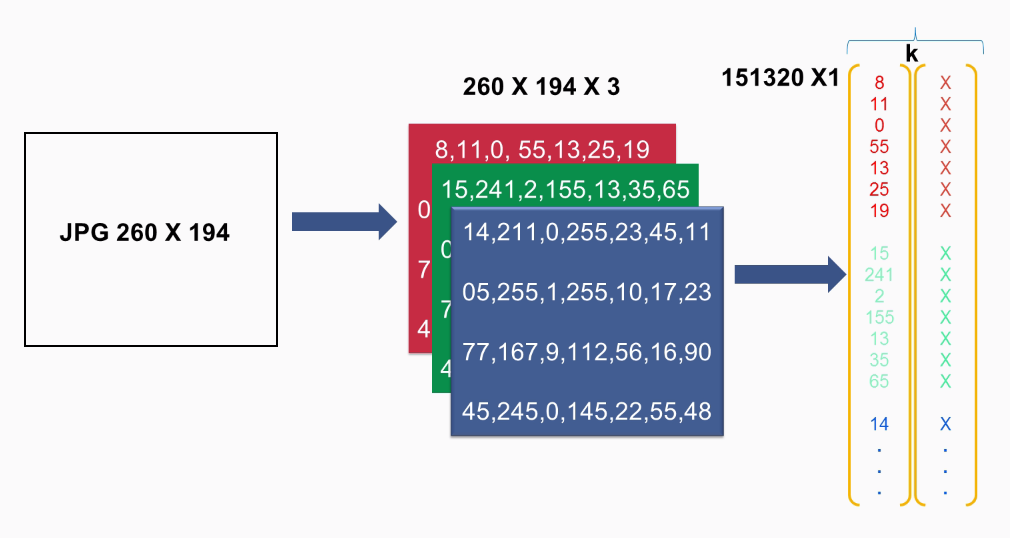
We can also add k-images by choosing mini-batch gradient descent and processing k-images in parallel.
Notice how the number of features dramatically increases for color images, from 784 to 150,000 features. Due to this, the processing time of the image increases drastically, which is where we need to implement techniques to increase the speed of our model.


























































 . Thus, we will have
. Thus, we will have  ,
,  , and
, and  , sum up this
, sum up this  equal to 148.4.
equal to 148.4.  equal to 7.4. Similarly,
equal to 7.4. Similarly,  will be equal to 0.4. The sum of these values is 156.2. The next step, as discussed, is dividing each of these values by the sum to attain the final percentages.
will be equal to 0.4. The sum of these values is 156.2. The next step, as discussed, is dividing each of these values by the sum to attain the final percentages.




