Optimizing model parameters
We've already seen that we need to tweak the weights and biases, collectively called the parameters, of our model in order to arrive at a closer approximation of our desired function.
In other words, we need to look through the space of possible functions that can be represented by our model in order to find a function, 
, that matches our desired function, f, as closely as possible.
But how would we know how close we are? In fact, since we don't know f, we cannot directly know how close our hypothesis, 
, is to f. But what we can do is measure how well 
's outputs match the output of f. The expected outputs of f given X are the labels, y. So, we can try to approximate f by finding a function, 
, whose outputs are also y given X.
We know that the following is true:
We also know that:
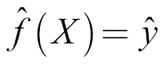
We can try to find f by optimizing using the following formula:
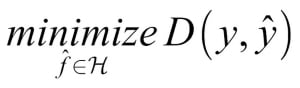
Within this formula, 
is the space of functions that can be represented by our model, also called the hypothesis space, while D is the distance function, which we use to evaluate how close 
and y are.
Note
Note: This approach makes a crucial assumption that our data, X, and labels, y, represent our desired function, f. This is not always the case. When our data contains systematic biases, we might gain a function that fits our data well but is different from the one we wanted.
An example of optimizing model parameters comes from human resource management. Imagine you are trying to build a model that predicts the likelihood of a debtor defaulting on their loan, with the intention of using this to decide who should get a loan.
As training data, you can use loan decisions made by human bank managers over the years. However, this presents a problem as these managers might be biased. For instance, minorities, such as black people, have historically had a harder time getting a loan.
With that being said, if we used that training data, our function would also present that bias. You'd end up with a function mirroring or even amplifying human biases, rather than creating a function that is good at predicting who is a good debtor.
It is a commonly made mistake to believe that a neural network will find the intuitive function that we are looking for. It'll actually find the function that best fits the data with no regard for whether that is the desired function or not.
