8.2 Elliptic curves as abelian groups
Two points P and Q on a smooth elliptic curve E in reduced Weierstrass form can be added to give another point R = P + Q on E. The addition process can be best understood by describing it as a geometrical recipe over the real numbers first.
8.2.1 Geometrical viewpoint
To find the sum of two points P and Q on E, we draw a line through P and Q first. One can show that this line must have exactly one additional intersection point with E. We find this point and form the mirror image of it with respect to the x axis by reversing the sign of its y coordinate. The result is the sum P + Q. This process is visualized in Figure 8.3.
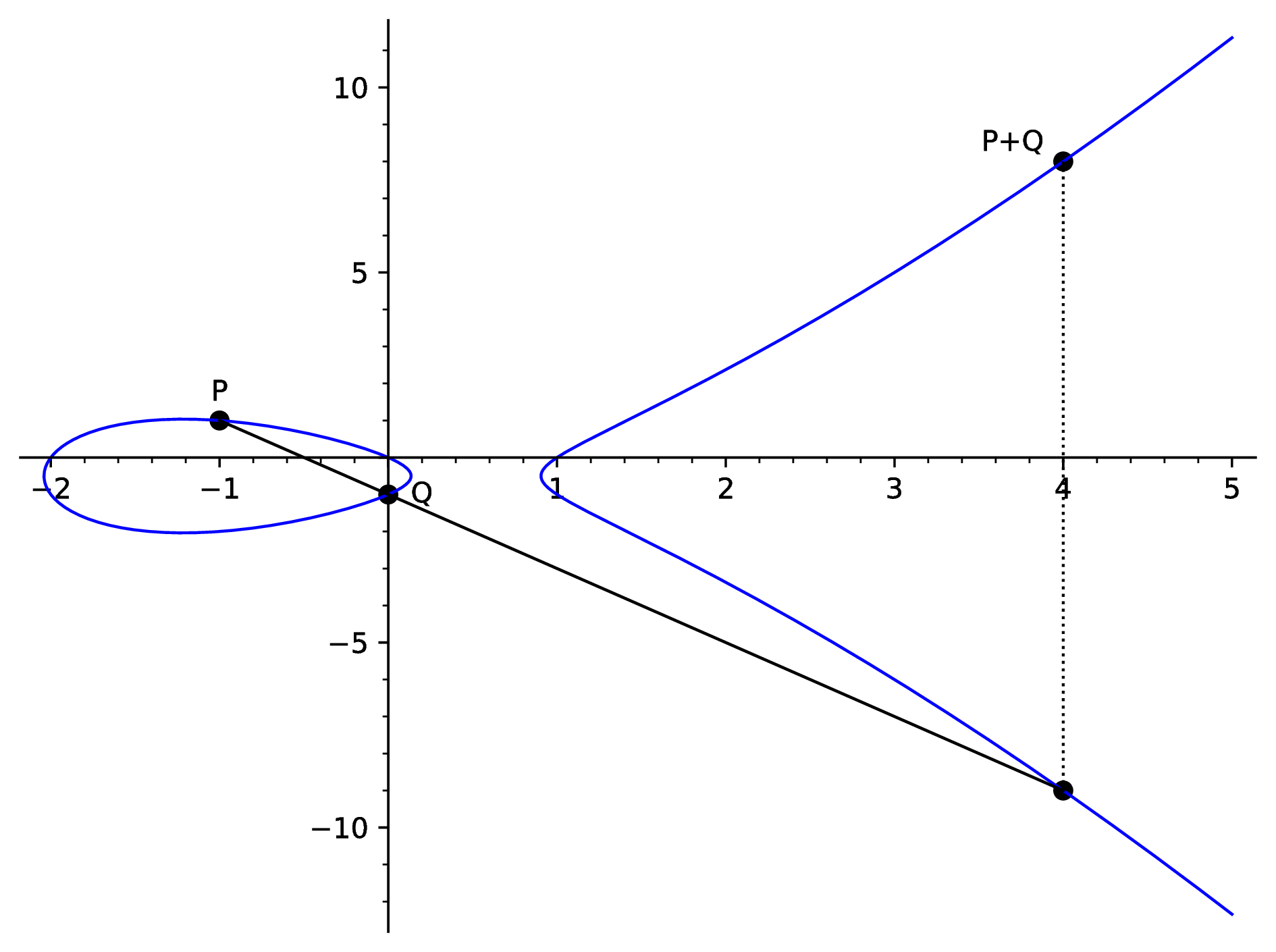
Figure 8.3: Elliptic curve point addition
Now let’s look at some special cases:
If P = Q, we form the tangent line t to E at P, find its intersection point with E and reverse the sign of its y coordinate. The result is the point P + P = 2P (see Figure 8.4).

Figure 8.4: Point doubling on an elliptic...
























































