Multiple Linear Regression

In the simple linear regression discussed previously, we only have one independent variable. If we include multiple independent variables in our analysis, we get a multiple linear regression model. Multiple linear regression is represented in a way that's similar to simple linear regression.

Let's consider a case where we want to fit a linear regression model that has three independent variables, X1, X2, and X3. The formula for the multiple linear regression equation will look like Equation 2.2:

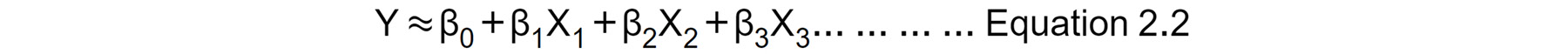
Figure 2.5: Multiple linear regression equation

Each independent variable will have its own coefficient or parameter (that is, β1 β2 or β3 ). The βs coefficient tells us how a change in their respective independent variable influences the dependent variable if all other independent variables are unchanged.

Estimating the Regression Coefficients (β0, β1, β2 and β3)

The regression coefficients in Equation 2.2 are estimated using the same least squares approach that was discussed when simple linear regression was introduced. To satisfy the least squares method, the chosen coefficients must minimize the sum of squared residuals.

Later in the chapter, we will make use of the Python programming language to compute these coefficient estimates practically.

Logarithmic Transformations of Variables

As has been mentioned already, sometimes the relationship between the dependent and independent variables is not linear. This limits the use of linear regression. To get around this, depending on the nature of the relationship, the logarithm function can be used to transform the variable of interest. What happens then is that the transformed variable tends to have a linear relationship with the other untransformed variables, enabling the use of linear regression to fit the data. This will be illustrated in practice on the dataset being analyzed later in the exercises of the book.

Correlation Matrices

In Figure 2.3, we saw how a linear relationship between two variables can be analyzed using a straight-line graph. Another way of visualizing the linear relationship between variables is with a correlation matrix. A correlation matrix is a kind of cross-table of numbers showing the correlation between pairs of variables, that is, how strongly the two variables are connected (this can be thought of as how a change in one variable will cause a change in the other variable). It is not easy analyzing raw figures in a table. A correlation matrix can, therefore, be converted to a form of "heatmap" so that the correlation between variables can easily be observed using different colors. An example of this is shown in Exercise 2.01.