8.2 Modeling functions
We will begin our discussion of Gaussian processes by first describing a way to represent functions as probabilistic objects. We may think of a function f as a mapping from a set of inputs X to a set of outputs Y . Thus, we can write:
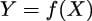
One very crude way to represent functions is by listing for each xi value its corresponding yi value as in Table 8.1. You may remember this way of representing functions from elementary school.
| x | y |
| 0.00 | 0.46 |
| 0.33 | 2.60 |
| 0.67 | 5.90 |
| 1.00 | 7.91 |
Table 8.1: A tabular representation of a function (sort of)
As a general case, the values of X and Y will live on the real line; thus, we can see a function as a (potentially) infinite and ordered list of paired values (xi,yi). The order is important because, if we shuffle the values, we will get different functions.
Following this description, we can represent, numerically, any specific function we want. But what if we want to represent functions probabilistically? Well,...























































