Graph representation

Graphs can be represented in two main forms. One way is to use an adjacency matrix and the other is to use an adjacency list.

We shall be working with the following figure to develop both types of representation for graphs:

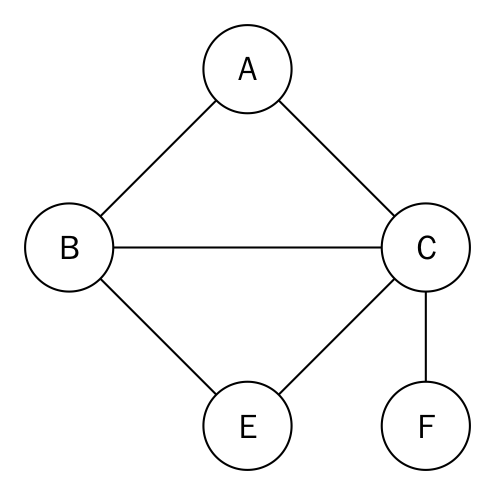
Adjacency list

A simple list can be used to present a graph. The indices of the list will represent the nodes or vertices in the graph. At each index, the adjacent nodes to that vertex can be stored:

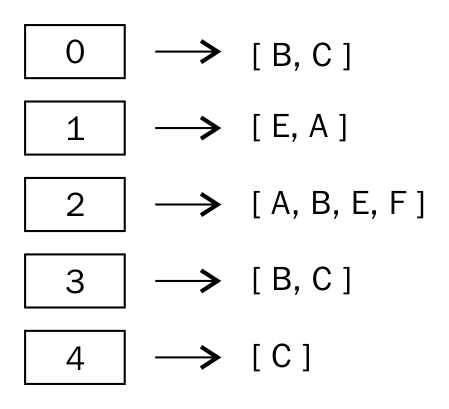
The numbers in the box represent the vertices. Index 0 represents vertex A, with its adjacent nodes being B and C.

Using a list for the representation is quite restrictive because we lack the ability to directly use the vertex labels. A dictionary is therefore more suited. To represent the graph in the diagram, we can use the following statements:

    graph = dict() 
    graph['A'] = ['B', 'C'] 
    graph['B'] = ['E','A'] 
    graph['C'] = ['A', 'B', 'E','F'] 
    graph['E'] = ['B', 'C'] 
    graph['F'] = ['C'] 

Now we easy establish that vertex A has the adjacent...