Exploring Discrete Event Simulation (DES)

A DES is a dynamic system whose states can assume logical or symbolic values rather than numerical ones. The behavior of the system is characterized by the occurrence of instantaneous events that arise with an irregular timing not necessarily known a priori. The behavior of such systems is described in terms of states and events.

A DES considers the system as a sequence of discrete events over time: each event occurs at a particular instant t and implements a change of state in the system. Therefore, between two consecutive events, it is assumed that there is no change of state, and therefore once the event is concluded at a certain instant t1, it is possible to go directly to the instant of the start of the next event t2.

In DES, the evolutions of the system over time are represented with variables that instantly change value in defined instants of time, included in a well-defined numerical interval, which determines the occurrence of events. The objects in a simulation system of this type are distinct elements, each having its own characteristics that determine its behavior within the model, which are called tokens. Discrete event simulation models are characterized by the following points:

• State variables that take on discrete values
• Transitions from one state to another that occur in discrete moments

To simulate a discrete event model, it is necessary to identify the state variables of the system and the classes of events that give rise to state transitions. Generally, in a discrete event simulation system, the state variables between one event and the next remain constant.

An example of a discrete event simulation is given by a queue of customers arriving at the checkout and needing to be served by one or more cashiers. In this case, the system entities are the customers in the queue and the cashiers. The events are only customer-approach and customer-leaves because we can include the cashier-serves-customer event in the logic of the other two. They implement a change in the states of the system; in this case, we can consider the following as states:

• The number of customers in the queue, represented by an integer from 0 to n
• The state of the cashier, represented by a Boolean variable that indicates whether it is free (F) or busy (B) (Figure 1.3)

The simulation also needs random variables: the first represents how often a new customer approaches, and the second is the time it takes the cashier to serve a customer.

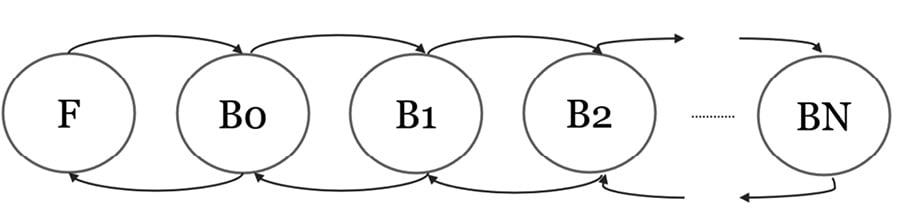
Figure 1.3: Transition diagram of cash desk queue

All events of a discrete event simulation system can be classified into the following categories:

• External events, independent of the behavior of the modeled system, are always present in the list of active events
• Internal events, which are a function of the system status, may or may not be present in the list of active events

The processes of arrival and departure of customers at a cash desk are completely characterized by probability distributions. It is essential to be able to evaluate, based on the data available, the probability distributions relating to the inter-arrival times of the tokens in the activities and the service of activities.

Another distinctive element of DES models is that the use of resources and activity times are specific to every single element of the system and are sampled using probability distributions. The rules governing the order in which the activities occur in the model are defined during the implementation phase of the model and are dependent on both how the workflow is structured and the characteristics of the individual entities.

The fundamental elements of a DES system are, therefore, the following:

• State Variables: Variables that describe the state of a system at any instant in time. In a DES model, the state variables take on discrete values, and the transitions from one state to another take place in discrete instants.
• Events: Any instantaneous occurrence that causes the value of at least one of the state variables to change.
• Activity: Temporal actions between two events, the duration of which is known a priori at the beginning of the execution of the activity.
• Entities and logical relationships: Entities are the tangible elements present in the real world, while logical relationships connect the different objects together, defining the general behavior of the model. Entities can be dynamic if they flow within the system or static entities. Entities can also be characterized by attributes that provide a data value assigned to the entity.
• Resources: Elements of the system that provide a service to entities.
• Simulation time: Keeps track of the logical relationships between entities in the time range to be simulated.

There are two ways to define the progress of the simulation time:

• Advancement of time to the next event: Time flows according to the events; it passes from the previous moment to the next one only according to the events associated with these moments
• Advancement of time in predetermined increments: Time flows regardless of the events; it passes from one instant before to the next regardless of the events associated with those instants

Finite-state machine (FSM)

To describe a DES in a simple way, we can adapt the FSM model. It is the first abstraction of a machine equipped with memory that executes algorithms. It introduces the fundamental concept of the state, which can be defined as a particular condition of the machine. As a result, the machine reacts with a certain output to a specific input. Since the output also depends on the state, FSM is an automaton intrinsically equipped with an internal memory that can therefore influence the answers given by the automaton. A system of this nature can be formally described with a quintuple of variables:

Here, we have the following variables:

• S is the finite set of possible states
• I is the possible set of input values
• O is the set of possible output values
• δ is the function that links inputs and the current state with the neighboring state
• is the initial state

The state contains the information necessary to calculate the system output, and in general, the inference of the sequence of inputs that brought the system to a certain state is not possible.

A system in which the output depends only on the current state is called Moore’s Machine. If the output depends on both the current state and the inputs, then it is called the Mealy Machine. In Moore’s machine, the outputs are connected to the current state of the system, whereas in Mealy’s machine, they are connected to the transitions from one state to another. The two automata are equivalent, that is, a system that can be created with one of the two models can always be created with the other model as well. In general, Mealy automata have fewer states than the corresponding Moore automata, even if they are more complicated to synthesize.

State transition table (STT)

The state of a state machine evolves in the presence of an event on the input or on the state itself. A sequential machine can be described by means of the state table. The column indices are the symbols of the input values, while the row indices are the state symbols that indicate, in the case of a Moore automaton, each possible current state, and for each combination of inputs, the next state reached by the automaton is indicated. Finally, a further column of the table expresses the relationship between the system status and the corresponding output.

State transition graph (STG)

The STG allows you to completely describe a finite state automaton through an oriented and labeled graph. It is a very useful graphic representation in the initial phases of the project, in which we pass from a formal description of the machine to its behavioral model. A node of the graph corresponds to each state. If a transition from state A to state B is possible in relation to input i, then on the graph, there will exist an arc oriented from the node corresponding to A to the node corresponding to B, labeled with i (Figure 1.2). In the case of Moore automata, in which the output is a function of the current state only, the indication of the output u corresponding to a state A is shown inside the node that identifies state A.

After exploring DES, we will now look at how to model dynamic systems.