Linear functionals
A linear functional is a special case of a linear transformation that takes in a vector and spits out a scalar:
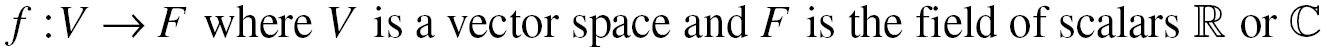
For instance, I could define a linear functional for every vector in ℝ2:
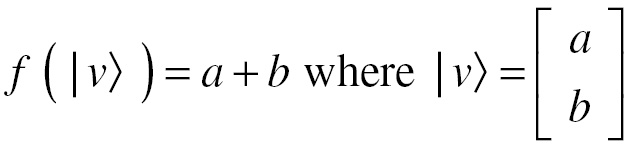
So that:
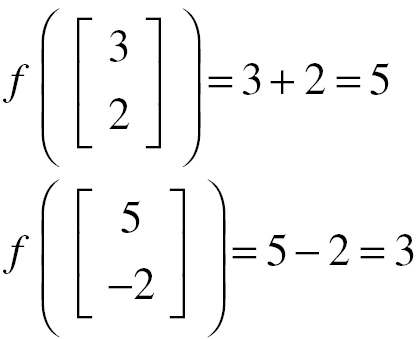
There are many linear functionals that can be defined for a vector space. Here's another one:
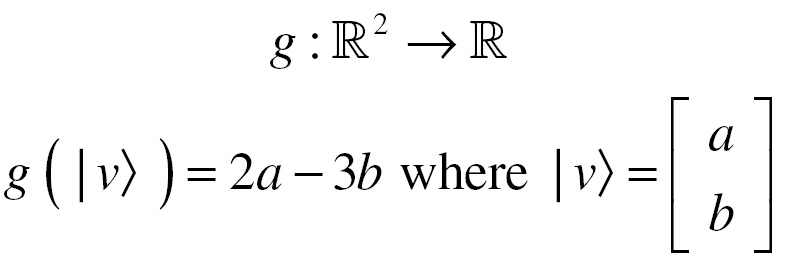
The set of all linear functionals that can be defined on a vector space actually form their own vector space called the dual vector space. This concept is important to fully define a bra in bra-ket notation. Please see the Appendix section on bra-ket notation if you are interested in more information.

































































