Understanding cubic Bézier splines
To implement game animation, you need some understanding of curves. Let's start with the basics—a cubic Bézier spline. A Bézier spline has two points to interpolate between and two control points that help generate a curve. This is what a cubic Bézier spline looks like:
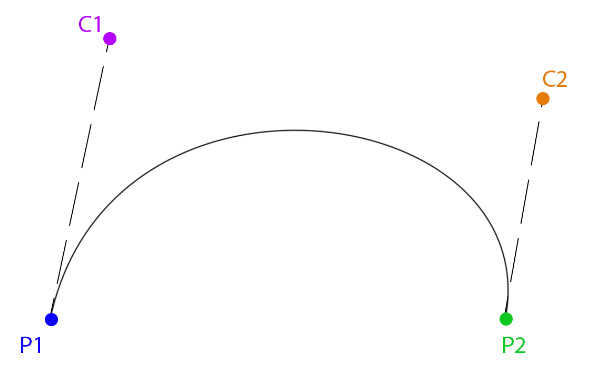
Figure 8.2: A cubic Bézier spline
Given the two points and the two controls, how is the curve generated? Let's explore interpolating the curve for a given time, t. Start by drawing a line from P1 to C1, from C1 to C2, and from C2 to P2. Then, linearly interpolate along those lines with the value of t:
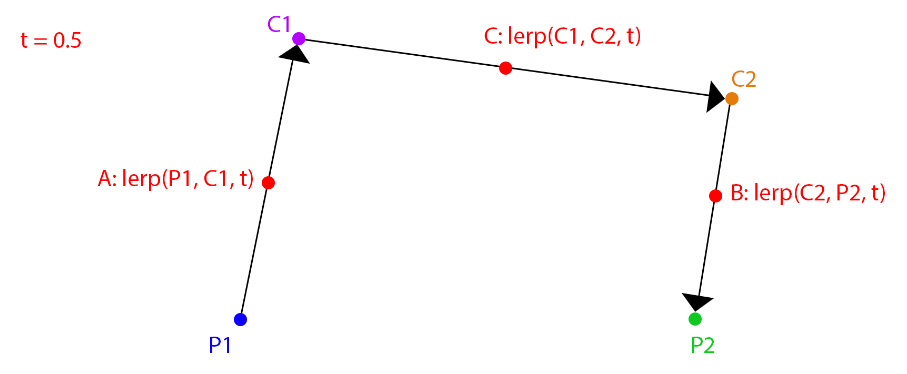
Figure 8.3: Linearly interpolating between points and control points
The interpolated points from P1 to C1 is A, from C2 to P2 is B, and from C1 to C2 is C. Next, you need to repeat this process, drawing lines and interpolating from A to C and from C to B. Let's call these newly...


























































